
题目列表(包括答案和解析)
抛物线经过点(2,-3),它与x轴交点的横坐标是-1和3.
(1)求抛物线的解析式;
(2)用配方法求出抛物线的对称轴方程和顶点坐标;
(3)画出草图;
(4)观察图象,x取何值时,函数值小于零?x取何值时,函数值随x的增大而减小?
在送医下乡活动中,某医院安排3名男医生和2名女医生到三所乡医院工作,每所医院至少安排一名医生,且女医生不安排在同一乡医院工作,则不同的分 配方法总数为( )
A.78 B.114 C.108 D. 120
用配方法解方程![]() ,配方后的方程是【 】
,配方后的方程是【 】
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
用配方法将函数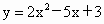 化成
化成 的形式,并指出它的开口方向,对称轴及顶点位置.
的形式,并指出它的开口方向,对称轴及顶点位置.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com