
题目列表(包括答案和解析)
 已知某人工养殖观赏鱼池塘中养殖着大量的红鲫鱼与中国金鱼.为了估计池塘中这两种鱼的数量,养殖人员从水库中捕出了红鲫鱼与中国金鱼各1000只,给每只鱼作上不影响其存活的记号,然后放回池塘,经过一定时间,再每次从池塘中随机地捕出1000只鱼,分类记录下其中有记号的鱼的数目,随即将它们放回池塘中.这样的记录作了10次,将记录获取的数据作成如图的茎叶图.
已知某人工养殖观赏鱼池塘中养殖着大量的红鲫鱼与中国金鱼.为了估计池塘中这两种鱼的数量,养殖人员从水库中捕出了红鲫鱼与中国金鱼各1000只,给每只鱼作上不影响其存活的记号,然后放回池塘,经过一定时间,再每次从池塘中随机地捕出1000只鱼,分类记录下其中有记号的鱼的数目,随即将它们放回池塘中.这样的记录作了10次,将记录获取的数据作成如图的茎叶图.| “厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
| 厨余垃圾 | 400 | 100 | 100 |
| 可回收物 | 30 | 240 | 30 |
| 其他垃圾 | 20 | 20 | 60 |
(本小题共12分)近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
|
|
“厨余垃圾”箱 |
“可回收物”箱 |
“其他垃圾”箱 |
|
厨余垃圾 |
400 |
100 |
100 |
|
可回收物 |
30 |
240 |
30 |
|
其他垃圾 |
20 |
20 |
60 |
(Ⅰ)试估计厨余垃圾投放正确的概率;
(Ⅱ)试估计生活垃圾投放错误的概率;
(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为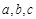 ,其中
,其中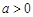 ,
,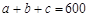 。当数据
。当数据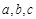 的方差
的方差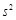 最大时,写出
最大时,写出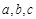 的值(结论不要求证明),并求此时
的值(结论不要求证明),并求此时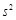 的值.
的值.
(注: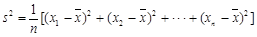 ,其中
,其中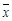 为数据
为数据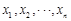 的平均数)
的平均数)
近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
|
|
“厨余垃圾”箱 |
“可回收物”箱 |
“其他垃圾”箱 |
|
厨余垃圾 |
400 |
100 |
100 |
|
可回收物 |
30 |
240 |
30 |
|
其他垃圾 |
20 |
20 |
60 |
(1)试估计厨余垃圾投放正确的概率;
(2)试估计生活垃圾投放错误的概率;
利用随机变量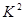 来判断“两个分类变量有
来判断“两个分类变量有 关系”的方法称为独立性检验,现通过计算高中生的性别与喜欢数学课程列联表中的数据,得到
关系”的方法称为独立性检验,现通过计算高中生的性别与喜欢数学课程列联表中的数据,得到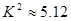 ,并且知道
,并且知道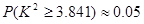 ,那么下列结论中正确的是
,那么下列结论中正确的是
A.100个高中生中只有5个不喜欢数学
B.100个高中生中只有5个喜欢数学
C.在犯错误的概率不超过0.05的前提下,可以认为高中生的性别与喜欢数学课程有关系
D.在犯错误的概率不超过0.05的前提下,可以认为高中生的性别与喜欢数学课程没有关系
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com