
题目列表(包括答案和解析)
(08年上海卢湾模拟)(10分)一同学想研究电梯上升过程的运动规律。某天乘电梯上楼时他携带了一个质量为5kg的砝码和一个量程足够大的弹簧秤,用手提着弹簧秤,砝码悬挂在秤钩上。电梯从第一层开始启动,中间不间断,一直到最高层停止。在这个过程中,他记录了弹簧秤在不同时段内的读数如表所示。取重力加速度g=10m/s2,根据表格中的数据,求:
时间/s | 弹簧秤示数/N |
电梯启动前 | 50.0 |
0~3.0 | 58.0 |
3.0~13.0 | 50.0 |
13.0~19.0 | 46.0 |
19.0以后 | 50.0 |
(2)电梯在3.0~13.0s时段内的速度v的大小;
(3)电梯在19.0s内上升的高度H。
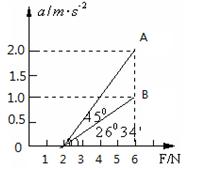
(08年上海黄埔模拟)(10分) 辨析题:物体A、B都静止在同一水平面上,它们的质量分别是mA和mB,与水平面之间的动摩擦因数分别为μA和μB。用平行于水平面的力F分别拉物体A、B,得到加速度a和拉力F的关系图象分别如图中A、B所示。利用图象求出A、B两物体与水平面之间动摩擦因数μA和μB的数值。
甲同学分析的过程是:从图象中得到F=6N时,A物体的加速度aA=2.0m/s2,B物体的加速度aB=1.0m/s2,根据牛顿定律导出:
![]()
又![]()
![]()
![]()
乙同学的分析过程是:从图象中得出直线A、B的斜率为:
kA=tan450=1, kB=tan26034’=0.5,
而斜率![]()
又![]()
![]()
![]()
你认为这两位同学的解法是否合理?请说明理由;若不合理,请用你自己的方法算出正确结果。
(08年上海卢湾模拟)(10分)如图所示,底面积s = 40cm2的圆柱形气缸C开口向上放置在水平地面上,内有一可自由移动的活塞封闭了一定质量的理想气体,不可伸长的细线一端系在质量为 2kg活塞上,另一端跨过两个定滑轮提着一轻弹簧B和质量也为 2kg的物体A。开始时,封闭气体的压强p1=1.0×105Pa,温度t1=7℃,活塞到缸底的距离l1=10cm,物体A的底部离地h1=2cm,弹簧的伸长量为2cm。已知外界大气压p0=1.0×105Pa不变。现对气缸内的气体缓慢加热,试求:
(1)当物体A刚触地时,气体的温度加热到了多少℃?
(2)当弹簧恰好恢复原长时,气体的温度加热到了多少℃?
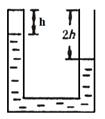
(08年上海黄埔模拟)(12分)在水平面竖直放置一个截面均匀等臂的U形玻璃管,管内盛有密度为![]() 的液体,如图所示,玻璃管的右侧上端开口,左侧上端封闭,左侧封闭的空气柱长度为h,右侧液面与管口相距高度为2h,在右侧液面上放置一个质量和厚度都可以忽略不计的活塞,它与管壁间既无摩擦又无间隙,从右端开口处缓慢注入密度为
的液体,如图所示,玻璃管的右侧上端开口,左侧上端封闭,左侧封闭的空气柱长度为h,右侧液面与管口相距高度为2h,在右侧液面上放置一个质量和厚度都可以忽略不计的活塞,它与管壁间既无摩擦又无间隙,从右端开口处缓慢注入密度为![]() 的液体,直到注满为止,注入液体后左侧空气气柱的长度为h/2,设在注入液体过程中,周围的温度不变,大气压强
的液体,直到注满为止,注入液体后左侧空气气柱的长度为h/2,设在注入液体过程中,周围的温度不变,大气压强![]() ,求:
,求:
(1)在右管中注入液体的高度;
(2)两种液体的密度之比![]() 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com