
题目列表(包括答案和解析)
(本小题满分13分)
为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽出取14件和5件,测量产品中的微量元素x,y的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
(1)已知甲厂生产的产品共有98件,求乙厂生产的产品数量;
(2)当产品中的微量元素x,y满足x≥175,且y≥75时,该产品为优等品。用上述样本数据估计乙厂生产的优等品的数量;
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数![]() 的分布列极其均值(即数学期望)。
的分布列极其均值(即数学期望)。
(本小题满分14分)
已知函数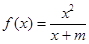 的图像经过点
的图像经过点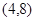 .
.
(1)求该函数的解析式;
(2)数列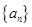 中,若
中,若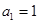 ,
,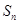 为数列
为数列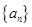 的前
的前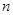 项和,且满足
项和,且满足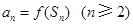 ,
,
证明数列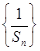 成等差数列,并求数列
成等差数列,并求数列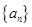 的通项公式;
的通项公式;
(3)另有一新数列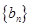 ,若将数列
,若将数列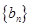 中的所有项按每一行比上一行多一项的规则排成
中的所有项按每一行比上一行多一项的规则排成
如下数表:
|
|
|
|
|
|
|
|
记表中的第一列数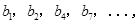 构成的数列即为数列
构成的数列即为数列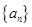 ,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当
,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当
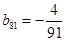 时,求上表中第
时,求上表中第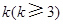 行所有项的和.
行所有项的和.
(本小题满分14分)
已知函数 的图像经过点
的图像经过点 .
.
(1)求该函数的解析式;
(2)数列 中,若
中,若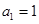 ,
, 为数列
为数列 的前
的前 项和,且满足
项和,且满足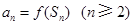 ,
,
证明数列 成等差数列,并求数列
成等差数列,并求数列 的通项公式;
的通项公式;
(3)另有一新数列 ,若将数列
,若将数列 中的所有项按每一行比上一行多一项的规则排成
中的所有项按每一行比上一行多一项的规则排成
如下数表:
 |
  |
   |
    |
 构成的数列即为数列
构成的数列即为数列 ,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当
,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当 时,求上表中第
时,求上表中第 行所有项的和.
行所有项的和. 的图像经过点
的图像经过点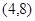 .
.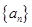 中,若
中,若 ,
,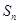 为数列
为数列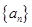 的前
的前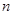 项和,且满足
项和,且满足 ,
,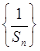 成等差数列,并求数列
成等差数列,并求数列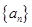 的通项公式;
的通项公式;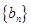 ,若将数列
,若将数列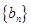 中的所有项按每一行比上一行多一项的规则排成
中的所有项按每一行比上一行多一项的规则排成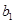 |
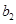 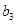 |
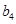 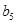 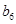 |
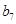 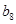  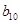 |
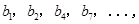 构成的数列即为数列
构成的数列即为数列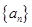 ,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当
,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当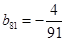 时,求上表中第
时,求上表中第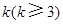 行所有项的和.
行所有项的和.已知递增等差数列 满足:
满足: ,且
,且 成等比数列.
成等比数列.
(1)求数列 的通项公式
的通项公式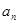 ;
;
(2)若不等式 对任意
对任意 恒成立,试猜想出实数
恒成立,试猜想出实数 的最小值,并证明.
的最小值,并证明.
【解析】本试题主要考查了数列的通项公式的运用以及数列求和的运用。第一问中,利用设数列 公差为
公差为 ,
,
由题意可知 ,即
,即 ,解得d,得到通项公式,第二问中,不等式等价于
,解得d,得到通项公式,第二问中,不等式等价于 ,利用当
,利用当 时,
时, ;当
;当 时,
时, ;而
;而 ,所以猜想,
,所以猜想, 的最小值为
的最小值为 然后加以证明即可。
然后加以证明即可。
解:(1)设数列 公差为
公差为 ,由题意可知
,由题意可知 ,即
,即 ,
,
解得 或
或 (舍去). …………3分
(舍去). …………3分
所以, . …………6分
. …………6分
(2)不等式等价于 ,
,
当 时,
时, ;当
;当 时,
时, ;
;
而 ,所以猜想,
,所以猜想, 的最小值为
的最小值为 . …………8分
. …………8分
下证不等式 对任意
对任意 恒成立.
恒成立.
方法一:数学归纳法.
当 时,
时, ,成立.
,成立.
假设当 时,不等式
时,不等式 成立,
成立,
当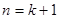 时,
时, ,
…………10分
,
…………10分
只要证  ,只要证
,只要证  ,
,
只要证  ,只要证
,只要证  ,
,
只要证  ,显然成立.所以,对任意
,显然成立.所以,对任意 ,不等式
,不等式 恒成立.…14分
恒成立.…14分
方法二:单调性证明.
要证 
只要证  ,
,
设数列 的通项公式
的通项公式 , …………10分
, …………10分
 , …………12分
, …………12分
所以对 ,都有
,都有 ,可知数列
,可知数列 为单调递减数列.
为单调递减数列.
而 ,所以
,所以 恒成立,
恒成立,
故 的最小值为
的最小值为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com