
题目列表(包括答案和解析)
在区间[-1,1]上随机取一个数x,即![]() 时,要使
时,要使![]() 的值介于0到
的值介于0到![]() 之间,需使
之间,需使![]() 或
或![]() ∴
∴![]() 或
或![]() ,区间长度为
,区间长度为![]() ,由几何概型知
,由几何概型知![]() 的值介于0到
的值介于0到![]() 之间的概率为
之间的概率为![]() .故选A.
.故选A.
答案:A
 【命题立意】:本题考查了三角函数的值域和几何概型问题,由自变量x的取值范围,得到函数值
【命题立意】:本题考查了三角函数的值域和几何概型问题,由自变量x的取值范围,得到函数值![]() 的范围,再由长度型几何概型求得.
的范围,再由长度型几何概型求得.
| 2 | 3 |

| 1 |
| 3 |
| 2 |
| 3 |
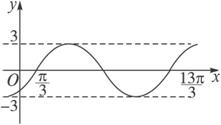
(1)用正弦函数写出其解析式;
(2)求图象与这个函数的图象关于直线x=2π对称的函数的解析式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com