
题目列表(包括答案和解析)
一种放射性元素,最初质量为500 g,按每年10%衰减.
(1)求t年后,这种放射性元素质量s的表达式;
(2)根据求出的函数表达式,求这种放射性元素的半衰期.(精确到十分位)
为了测试某种金属的热膨胀性质,将这种金属的一根细棒加热,从100℃开始第一次量细棒的长度,以后每升高50℃量一次,把依次量得的数据所成的数列{ln}表示成图象,如图所示.根据图象解答下列问题:

(1)第5次量的金属的长度是多少?此时金属棒的温度是多少?
(2)求{ln}的通项公式和金属棒长度l(单位:m)关于温度t(单位:℃)的函数关系式(设长度是关于温度的线性函数);
(3)在30℃的温度条件下,如果把两块这种矩形金属板平铺在一个平面上,这个平面的最高温度可达到500℃,问铺设时两块金属板之间至少要留出多宽的空隙?
 ,并且当n>1且n∈N*时,满足
,并且当n>1且n∈N*时,满足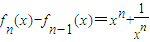 .
.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com