【答案】
分析:(1)利用累加法直接求函数f
n(x)(n∈N
*)的解析式;
(2)当n=1当n=1,2,3时,分别利用双勾函数,平方,求出函数f
1(x),f
2(x),f
3(x)的单调性与值域;
(3)借助(2)的研究过程或研究结论,求出第一类,结论一:f
4(x)单调性与值域;结论二:f
5(x)的单调性与值域;第二类问题,结论三、当x>0时,函数f
n(x)的单调性与值域;结论四、当x<0且n为奇数时,结论五、当x<0且n为偶数时,函数f
n(x)的单调性与值域;通过数列求和,利用函数的单调性的定义证明即可…
解答:解:(1)由于
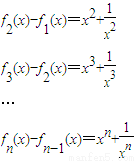
; (2分)
所以
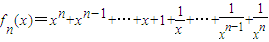
; (4分)
(2)(每小题结论正确(1分),证明(1分),共6分)
当n=1时,
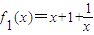
,易证函数的单调递增区间为(-∞,-1),(1,+∞);
单调递减区间为(-1,0),(0,1);值域为(-∞,-1]∪[3,+∞)
当n=2时,
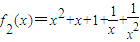

,易证函数的单调递增区间为(-1,0),(1,+∞;单位递减区间为(-∞,-1),(0,1);因此函数在(-∞,0)值域为[f
2(-1),+∞),在(0,+∞)上值域为[5,+∞)
因此函数

值域为[1,+∞)
当n=3时,
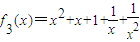
+
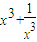
=f
2(x)+
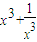
易证f
2(x)、
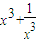
,在(0,1)单调递减,在(1,+∞)单调递增,
所以
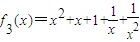
+
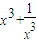
在(0,1)单调递减,在(1,+∞)单调递增.
由于

=
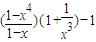
,用定义易证
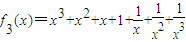
在(-∞,-1)单调递增,在(-1,0)上单调递减.
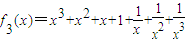
的值域为(-∞,-1]∪[7,+∞)
(3)以下给出若干解答供参考,评分方法参考本小题阅卷说明:
第一类问题
结论一、
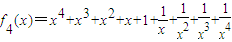
单调递增区间为(-1,0),(1,+∞)单调递减区间为(-∞,-1),(0,1);值域为[1,+∞);
结论二、
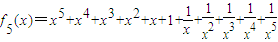
单调递增区间为(-∞,-1),(1,+∞)
;单调递减区间为(0,1),(-1,0),值域为(-∞,-1]∪[11,+∞)
解法及评分说明:解法与
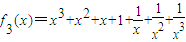
类同,结论分2分,证明正确得2分,共4分;
第二类问题
结论三、当x>0时,
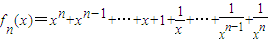
在(0,1)单调递减,在(1,+∞)单调递增,值域为[2n+1,+∞)
结论四、当x<0且n为奇数时,
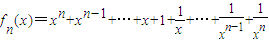
在(-1,0)单调递减,在(-∞,-1)单调递增;值域为(-∞,-1];
结论五、当x<0且n为偶数时,

在(-∞,-1)单调递减,在(-1,0)单调递增;值域为[1,+∞);
解法及评分说明:结论三的单调性证明可以用数学归纳法完成;即;x>0时.
①当n=1时,
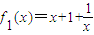
,用定义易证函数在(0,1)单调递减;在(1,+∞)上单调递增;计算得值域为(-∞,-1]∪[3,+∞)
②设函数

(n∈N
*)在(0,1)单调递减;在(1,+∞)
上单调递增;计算得值域为[2n+1,+∞)
则f
n+1(x)=f
n(x)+
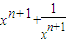
,对于任意0<x
1<x
2,f
n+1(x
2)-f
n+1(x
1)
=
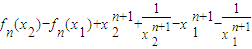
=
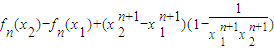
,易证函数f
n+1(x)=f
n(x)+
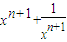
在(0,1)
单调递减,在(1,+∞)上单调递增;值域为[2(n+1)+1,+∞).
所以由①、②可得结论成立.
结论四及结论五的证明,可以先求和,后用定义进行证明,即:
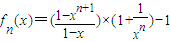
,
f
n(x
2)-f
n(x
1)=
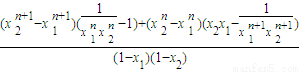
,容易获得结论的证明.
解法及评分说明:结论分3分,证明正确得3分,共6分;
第三类问题
结论六:当n为奇数时,

在(-1,0),(0,1)
单调递减,在(-∞,-1),(1,+∞)单调递增;值域为(-∞,-1]∪[2n+1,+∞);
结论七:当n为偶数时单调递增区间为(-1,0),(1,+∞),单调递减区间为(-∞,-1),(0,1)
;值域为[1,+∞);
结论八:当n为奇数时,
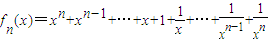
在(-1,0),(0,1)单调递减,在(-∞,-1),(1,+∞)单调递增;值域为(-∞,-1]∪[2n+1,+∞);
当n为偶数时单调递增区间为(-1,0),(1,+∞),单调递减区间为(-∞,-1),(0,1);值域为[1,+∞);
解法及评分说明:解法与第二类问题类同.结论分4分,求解正确得4分,共8分.
点评:本题是开放性问题,通过研究基本函数的单调性,类比到其它的情况,考查分类讨论的思想,函数的单调性的基本证明方法,转化思想的应用,数列求和的应用,难度大,综合性强,多作为压轴题目,竞赛试题出现.

 ,并且当n>1且n∈N*时,满足
,并且当n>1且n∈N*时,满足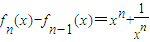 .
.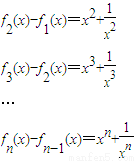 ; (2分)
; (2分)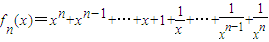 ; (4分)
; (4分)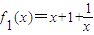 ,易证函数的单调递增区间为(-∞,-1),(1,+∞);
,易证函数的单调递增区间为(-∞,-1),(1,+∞);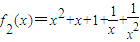
 ,易证函数的单调递增区间为(-1,0),(1,+∞;单位递减区间为(-∞,-1),(0,1);因此函数在(-∞,0)值域为[f2(-1),+∞),在(0,+∞)上值域为[5,+∞)
,易证函数的单调递增区间为(-1,0),(1,+∞;单位递减区间为(-∞,-1),(0,1);因此函数在(-∞,0)值域为[f2(-1),+∞),在(0,+∞)上值域为[5,+∞) 值域为[1,+∞)
值域为[1,+∞)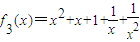 +
+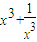 =f2(x)+
=f2(x)+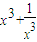
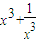 ,在(0,1)单调递减,在(1,+∞)单调递增,
,在(0,1)单调递减,在(1,+∞)单调递增,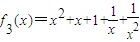 +
+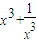 在(0,1)单调递减,在(1,+∞)单调递增.
在(0,1)单调递减,在(1,+∞)单调递增. =
=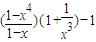 ,用定义易证
,用定义易证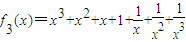 在(-∞,-1)单调递增,在(-1,0)上单调递减.
在(-∞,-1)单调递增,在(-1,0)上单调递减.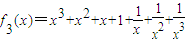 的值域为(-∞,-1]∪[7,+∞)
的值域为(-∞,-1]∪[7,+∞)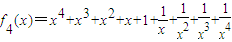 单调递增区间为(-1,0),(1,+∞)单调递减区间为(-∞,-1),(0,1);值域为[1,+∞);
单调递增区间为(-1,0),(1,+∞)单调递减区间为(-∞,-1),(0,1);值域为[1,+∞);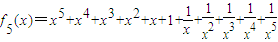 单调递增区间为(-∞,-1),(1,+∞)
单调递增区间为(-∞,-1),(1,+∞)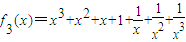 类同,结论分2分,证明正确得2分,共4分;
类同,结论分2分,证明正确得2分,共4分;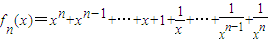
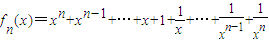 在(-1,0)单调递减,在(-∞,-1)单调递增;值域为(-∞,-1];
在(-1,0)单调递减,在(-∞,-1)单调递增;值域为(-∞,-1]; 在(-∞,-1)单调递减,在(-1,0)单调递增;值域为[1,+∞);
在(-∞,-1)单调递减,在(-1,0)单调递增;值域为[1,+∞);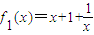 ,用定义易证函数在(0,1)单调递减;在(1,+∞)上单调递增;计算得值域为(-∞,-1]∪[3,+∞)
,用定义易证函数在(0,1)单调递减;在(1,+∞)上单调递增;计算得值域为(-∞,-1]∪[3,+∞) (n∈N*)在(0,1)单调递减;在(1,+∞)
(n∈N*)在(0,1)单调递减;在(1,+∞)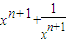 ,对于任意0<x1<x2,fn+1(x2)-fn+1(x1)
,对于任意0<x1<x2,fn+1(x2)-fn+1(x1) 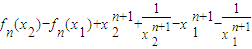
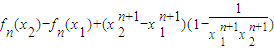 ,易证函数fn+1(x)=fn(x)+
,易证函数fn+1(x)=fn(x)+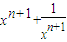 在(0,1)
在(0,1)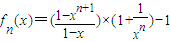 ,
,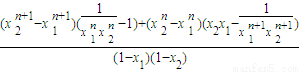 ,容易获得结论的证明.
,容易获得结论的证明. 在(-1,0),(0,1)
在(-1,0),(0,1) 在(-1,0),(0,1)单调递减,在(-∞,-1),(1,+∞)单调递增;值域为(-∞,-1]∪[2n+1,+∞);
在(-1,0),(0,1)单调递减,在(-∞,-1),(1,+∞)单调递增;值域为(-∞,-1]∪[2n+1,+∞);
