(1)由于
| | f2(x)-f1(x)=x2+ | | f3(x)-f2(x)=x3+ | | … | | fn(x)-fn-1(x)=xn+ |
| |
; (2分)
所以
fn(x)=xn+xn-1+…+x+1++…++; (4分)
(2)(每小题结论正确(1分),证明(1分),共6分)
当n=1时,
f1(x)=x+1+,易证函数的单调递增区间为(-∞,-1),(1,+∞);
单调递减区间为(-1,0),(0,1);值域为(-∞,-1]∪[3,+∞)
当n=2时,
f2(x)=x2+x+1++f2(x)=(x++)2-,易证函数的单调递增区间为(-1,0),(1,+∞;单位递减区间为(-∞,-1),(0,1);因此函数在(-∞,0)值域为[f
2(-1),+∞),在(0,+∞)上值域为[5,+∞)
因此函数
f2(x)=x2+x+1++值域为[1,+∞)
当n=3时,
f3(x)=x2+x+1+++
x3+=f
2(x)+
x3+易证f
2(x)、
x3+,在(0,1)单调递减,在(1,+∞)单调递增,
所以
f3(x)=x2+x+1+++
x3+在(0,1)单调递减,在(1,+∞)单调递增.
由于
f3(x)=x3+x2+x+1+++=
()(1+)-1,用定义易证
f3(x)=x3+x2+x+1+++在(-∞,-1)单调递增,在(-1,0)上单调递减.
f3(x)=x3+x2+x+1+++的值域为(-∞,-1]∪[7,+∞)
(3)以下给出若干解答供参考,评分方法参考本小题阅卷说明:
第一类问题
结论一、
f4(x)=x4+x3+x2+x+1++++单调递增区间为(-1,0),(1,+∞)单调递减区间为(-∞,-1),(0,1);值域为[1,+∞);
结论二、
f5(x)=x5+x4+x3+x2+x+1+++++单调递增区间为(-∞,-1),(1,+∞)
;单调递减区间为(0,1),(-1,0),值域为(-∞,-1]∪[11,+∞)
解法及评分说明:解法与
f3(x)=x3+x2+x+1+++类同,结论分2分,证明正确得2分,共4分;
第二类问题
结论三、当x>0时,
fn(x)=xn+xn-1+…+x+1++…++在(0,1)单调递减,在(1,+∞)单调递增,值域为[2n+1,+∞)
结论四、当x<0且n为奇数时,
fn(x)=xn+xn-1+…+x+1++…++在(-1,0)单调递减,在(-∞,-1)单调递增;值域为(-∞,-1];
结论五、当x<0且n为偶数时,
fn(x)=xn+xn-1+…+x+1++…++在(-∞,-1)单调递减,在(-1,0)单调递增;值域为[1,+∞);
解法及评分说明:结论三的单调性证明可以用数学归纳法完成;即;x>0时.
①当n=1时,
f1(x)=x+1+,用定义易证函数在(0,1)单调递减;在(1,+∞)上单调递增;计算得值域为(-∞,-1]∪[3,+∞)
②设函数
fn(x)=xn+xn-1+…+x+1++…++(n∈N
*)在(0,1)单调递减;在(1,+∞)
上单调递增;计算得值域为[2n+1,+∞)
则f
n+1(x)=f
n(x)+
xn+1+,对于任意0<x
1<x
2,f
n+1(x
2)-f
n+1(x
1)
=
fn(x2)-fn(x1)++-- =
fn(x2)-fn(x1)+(-)(1-),易证函数f
n+1(x)=f
n(x)+
xn+1+在(0,1)
单调递减,在(1,+∞)上单调递增;值域为[2(n+1)+1,+∞).
所以由①、②可得结论成立.
结论四及结论五的证明,可以先求和,后用定义进行证明,即:
fn(x)=()×(1+)-1,
f
n(x
2)-f
n(x
1)=
| (-)(-1)+(-)(x2x1-) |
| (1-x1)(1-x2) |
,容易获得结论的证明.
解法及评分说明:结论分3分,证明正确得3分,共6分;
第三类问题
结论六:当n为奇数时,
fn(x)=xn+xn-1+…+x+1++…++在(-1,0),(0,1)
单调递减,在(-∞,-1),(1,+∞)单调递增;值域为(-∞,-1]∪[2n+1,+∞);
结论七:当n为偶数时单调递增区间为(-1,0),(1,+∞),单调递减区间为(-∞,-1),(0,1)
;值域为[1,+∞);
结论八:当n为奇数时,
fn(x)=xn+xn-1+…+x+1++…++在(-1,0),(0,1)单调递减,在(-∞,-1),(1,+∞)单调递增;值域为(-∞,-1]∪[2n+1,+∞);
当n为偶数时单调递增区间为(-1,0),(1,+∞),单调递减区间为(-∞,-1),(0,1);值域为[1,+∞);
解法及评分说明:解法与第二类问题类同.结论分4分,求解正确得4分,共8分.



 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 ,并且当n>1且n∈N*时,满足
,并且当n>1且n∈N*时,满足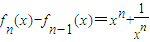 .
.