
题目列表(包括答案和解析)
 “数形结合”是一种极其重要的思想方法.例如,我们可以利用数轴解分式不等式
“数形结合”是一种极其重要的思想方法.例如,我们可以利用数轴解分式不等式| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |

 “数形结合”是一种极其重要的思想方法.例如,我们可以利用数轴解分式不等式
“数形结合”是一种极其重要的思想方法.例如,我们可以利用数轴解分式不等式 <1(x≠0).先考虑不等式的临界情况:方程
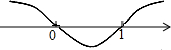
<1(x≠0).先考虑不等式的临界情况:方程 =1的解为x=1.如图,数轴上表示0和1的点将数轴“分割”成x<0、0<x<1和x>1三部分(0和1不算在内),依次考察三部分的数可得:当x<0和x>1时,
=1的解为x=1.如图,数轴上表示0和1的点将数轴“分割”成x<0、0<x<1和x>1三部分(0和1不算在内),依次考察三部分的数可得:当x<0和x>1时, <1成立.理解上述方法后,尝试运用“数形结合”的方法解决下列问题:
<1成立.理解上述方法后,尝试运用“数形结合”的方法解决下列问题: >1的解集是______;
>1的解集是______;(1)6位新同学参加夏令营,大家彼此握手,互相介绍自己,这6位同学共握手多少次?
小莉是这样思考的:每一位同学要与其他5位同学握手5次,6位同学握手5×6=30次,但每两位同学握手2次,因此这6位同学共握手![]() =15次.
=15次.
依此类推,12位同学彼此握手,共握手________次.
(2)我们经常会遇到与上面类似的问题,如:
2条直线相交,最多只有1个交点;3条直线相交,最多有3个交点;……;求20条直线相交,最多有多少个交点?
(3)在上述问题中,分别把人、线看成是研究对象,两人握手、两线相交是研究对象间的一种关系,要求的握手总次数、最多交点数就是求所有对象间的不同关系总数.它们都是满足一种相同的模型.请结合你学过的数学知识和生活经验,编制一个符合上述模型的问题.
(4)请运用解决上述问题的思想方法,探究n边形共有多少条对角线?写出你的探究过程及结果.
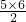 =15次.依此类推,12位同学彼此握手,共握手________次.
=15次.依此类推,12位同学彼此握手,共握手________次.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com