
题目列表(包括答案和解析)
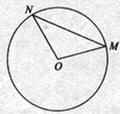
如图:![]() 是半径为
是半径为![]() 的圆周上一个定点,在圆周上等可能的任取一点
的圆周上一个定点,在圆周上等可能的任取一点![]() ,连接
,连接![]() ,则弦
,则弦![]() 的长度超过
的长度超过![]() 的概率是 .
的概率是 .
![]()
 如图是一幅招贴画的示意图,其中ABCD是边长为2a的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为l,∠APH=θ,θ∈(
如图是一幅招贴画的示意图,其中ABCD是边长为2a的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为l,∠APH=θ,θ∈(| π |
| 4 |
| 3π |
| 4 |
| OP |
| l |
| π |
| 4 |
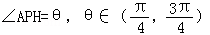 .
.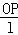 为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角θ满足:
为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角θ满足: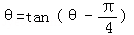 时,招贴画最优美.
时,招贴画最优美.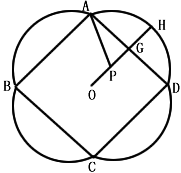
 .(1)求l关于θ的函数关系式;(2)定义比值
.(1)求l关于θ的函数关系式;(2)定义比值 为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角θ满足:
为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角θ满足: 时,招贴画最优美.
时,招贴画最优美.
如图是一幅招贴画的示意图,其中ABCD是边长为2a的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为l,∠APH=![]() ,
,![]() ∈(
∈(![]() ).
).

(1)求l关于![]() 的函数关系式;
的函数关系式;
(2)定义比值![]() 为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角
为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角![]() 满足:
满足:![]() =tan(
=tan(![]() -
-![]() )时,招贴画最优美.
)时,招贴画最优美.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com