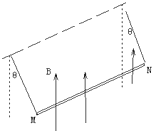如图所示，金属棒MN两端由等长的轻质细线水平悬挂，处于竖直向上的匀强磁场中，棒中通以由M向N的电流．平衡时两悬线与竖直方向夹角均为θ．如果仅改变下列某一个条件，θ的相应变化情况是（　　）

A．棒中的电流变大，θ角变小

B．两悬线等长变短，θ角不变

C．金属棒质量变大，θ角变大

D．磁感应强度变大，θ角变小

查看答案和解析>>

如图所示，在光滑的水平地面上，质量为M=3.0kg的长木板A的左端，叠放着一个质量为m=1.0kg的小物块B（可视为质点），处于静止状态，小物块与木板之间的动摩擦因数μ=0.30．在木板A的左端正上方，用长为R=0.80m不可伸长的轻绳将质量为m=1.0kg的小球C悬于固定点O．现将小球C拉至上方与水平方向成θ=30⁰角的位置，由静止释放，在将绳拉直的瞬间，小球C沿绳方向的分速度立刻减为零，而沿切线方向的分速度不变．此后，小球C与B恰好发生正碰且无机械能损失．空气阻力不计，取g=10m/s²． 求：
（1）小球运动到最低点时对细线的拉力；
（2）木板长度L至少为多大时小物块才不会滑出木板？

查看答案和解析>>

如图所示，一根长为L的轻质细线，一端固定于O点，另一端拴有一质量为m的小球，可在竖直的平面内绕O点摆动，现拉紧细线使小球位于与O点在同一竖直面内的A位置，细线与水平方向成30°角，从静止释放该小球，当小球运动至悬点正下方C位置时的速度是（　　）

A． 5gL 2

B． 5gL 2

C． 3gL

D． 3gL 2

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

一、选择题

1．BD 

2．BC 

3．AB 

4．C 

5．A 

6．CD 

7．A 

8．B 

9． CD 

10．CD 

11．B 

12．C

二、填空题

13．3n

14（1）如下表（3分）（2）E_k=kω  k=2Js/rad（3分）；（3）2rad/s（3分）

（rad/s）

   0.5

    1

    2

    3

    4

    n

    5

    20

    80

   180

   320

E（J）

0.5

2

8

18

32

三、计算题

16．(1)假设地球质量为M    有g=GM/R²

   设月球绕地球运动的轨道半径为r   有GMm_月/r²=m_月r(2π/T)² 

      由上面可得：r=    

(2) 设下落到月面的时间为t      有h=g_月t²/2    s= v₀t  

          可得：g_月=2h v₀²/s²       有g_月=G M_月/R_月²

M_月=2h R_月² v₀²/Gs²     (2分)

17、解:(1)mgl=mv²   1分            T₁-mg=m    1分

T₂-mg=m   1分    ∴T₁=3mg  1分  T₂=5mg    1分

(2)小球恰好能在竖直平面内做圆周运动，在最高点时有速度v₁，此时做圆周运动的半径为r，则mg(-r)= mv₁²    ①  1分          且mg=m   ②   1分

  由几何关系:X²=(L-r)²-()²    ③    1分

  由以上三式可得：r= L/3    ④    1分       x=L    ⑤   1分

(3)小球做圆周运动到达最低点时，速度设为v₂    则

T-mg=m    ⑥   1分  以后小球做平抛运动过B点，在水平方向有x=v₂t  ⑦ 1分

在竖直方向有：L/2-r=gt²    ⑧ 1分   由④⑤⑥⑦⑧式可得T=mg  2分

18、（1）L＝v₀t，1分    L＝＝，2分

所以E＝，1分

qEL＝E_kt－E_k，1分

所以E_kt＝qEL＋E_k＝5E_k，1分

（2）若粒子由bc边离开电场，L＝v₀t，v_y＝＝，2分

E_k’－E_k＝mv_y²＝＝，2分

所以E＝，1分

若粒子由cd边离开电场，

qEL＝E_k’－E_k，所以E＝，2分

19A、解：（1）小滑块从C到B的过程中，只有重力和电场力对它做功，设滑块经过圆弧轨道B点时的速度为v_B，根据动能定理有                       （2分）

解得                                             （2分）

（2）根据牛顿运动定律有                              （2分）

解得 N_B=3mg-2qE                                                     （2分）

（3）小滑块在AB轨道上运动时，所受摩擦力为 f=μmg                   （1分）

小滑块从C经B到A的过程中，重力做正功，电场力和摩擦力做负功。设小滑块在水平轨道上运动的距离（即A、B两点之间的距离）为L，则根据动能定理有

mgR-qE（R+L）-μmgL=0                                               （2分）

解得                                                （2分）