
题目列表(包括答案和解析)
(本题满分12分)已知函数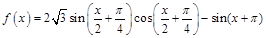 。
。
(1)求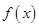 的最小正周期;
的最小正周期;
(2)若将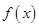 的图象向右平移
的图象向右平移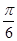 个单位,得到函数
个单位,得到函数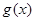 的图象,求函数
的图象,求函数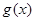 在区间
在区间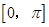 上的最大值和最小值。
上的最大值和最小值。
【解析】第一问中主要利用三角函数的两角和差公式化简为单一三角函数解析式
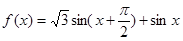 =
=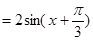
然后利用周期公式得到第一问。
第二问中,由于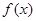 的图象向右平移
的图象向右平移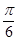 个单位,得到函数
个单位,得到函数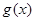 的图象,
的图象,
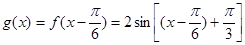
然后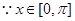 时,
时,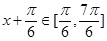 结合三角函数值域求解得到范围。
结合三角函数值域求解得到范围。
已知函数y=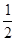 cos2x+
cos2x+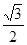 sinxcosx+1,x∈R.
sinxcosx+1,x∈R.
(1)求函数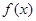 的最小正周期;
的最小正周期;
(2)求函数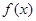 的单调减区间.
的单调减区间.
【解析】第一问中利用化为单一三角函数y=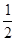 sin(2x+
sin(2x+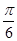 )+
)+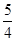 .,然后利用周期公式求解得到。第二问中,2x+
.,然后利用周期公式求解得到。第二问中,2x+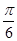 落在正弦函数的增区间里面,解得的x的范围即为所求,
落在正弦函数的增区间里面,解得的x的范围即为所求,
解:因为y=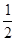 cos2x+
cos2x+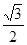 sinxcosx+1,x∈R.所以y=
sinxcosx+1,x∈R.所以y=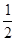 sin(2x+
sin(2x+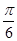 )+
)+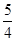 .
.
(1)周期为T=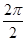 =π,
=π,
(2) 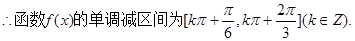
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com