
题目列表(包括答案和解析)
在平面直角坐标系中,点P(x,y)的几种特殊的对称点的坐标如下:
(1)关于原点的对称点是![]() (-x,-y)
(-x,-y)
(2)关于x轴的对称点是![]() (x,-y)
(x,-y)
(3)关于y轴的对称点是P?(-x,y)
那么,在空间直角坐标系内,点P(x,y,z)的几种特殊的对称点坐标:
(1)关于原点的对称点是P1________;
(2)关于横轴(x轴)的对称点是P2________;
(3)关于纵轴(y轴)的对称点是P3________;
(4)关于竖轴(z轴)的对称点是P4________;
(5)关于xOy坐标平面的对称点是P5________;
(6)关于yOz坐标平面的对称点P6________;
(7)关于zOx坐标平面的对称点是P7________.
在平面直角坐标系中,点P(x,y)的几种特殊的对称点的坐标如下:
(1)关于原点的对称点是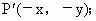
(2)关于x轴的对称点是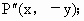
(3)关于y轴的对称点是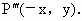
那么,在空间直角坐标系中,点P(x,y,z)的几种特殊的对称点坐标:
(1)关于原点的对称点是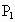 ______;
______;
(2)关于横轴(x轴)的对称点是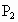 ______;
______;
(3)关于纵轴(y轴)的对称点是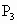 ______;
______;
(4)关于竖轴(z轴)的对称点是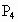 ______;
______;
(5)关于xOy坐标平面的对称点是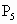 ______;
______;
(6)关于yOz坐标平面的对称点是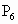 ______;
______;
(7)关于zOx坐标平面的对称点是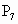 ______.
______.
请拓展思维及空间想象能力,准确解答本题.
在平面直角坐标系中,点
P(x,y)的几种特殊的对称点的坐标如下:(1)
关于原点的对称点是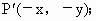
(2)
关于x轴的对称点是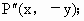
(3)
关于y轴的对称点是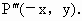
那么,在空间直角坐标系中,点
P(x,y,z)的几种特殊的对称点坐标:(1)
关于原点的对称点是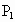 ______;
______;
(2)
关于横轴(x轴)的对称点是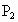 ______;
______;
(3)
关于纵轴(y轴)的对称点是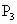 ______;
______;
(4)
关于竖轴(z轴)的对称点是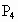 ______;
______;
(5)
关于xOy坐标平面的对称点是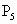 ______;
______;
(6)
关于yOz坐标平面的对称点是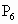 ______;
______;
(7)
关于zOx坐标平面的对称点是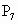 ______.
______.
请拓展思维及空间想象能力,准确解答本题.
| 2 | 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com