
题目列表(包括答案和解析)
(
荆州中学模拟)已知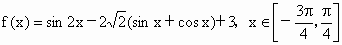 ,
,
(1)
求f(x)的最大值;(2)
若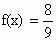 ,求cos2x的值.
,求cos2x的值.| 3 | 4 |
 (2008•临沂二模)为了了解中学生的身体发育情况,对某一中学同年龄的50名男生的身高进行了测量,结果如下:
(2008•临沂二模)为了了解中学生的身体发育情况,对某一中学同年龄的50名男生的身高进行了测量,结果如下:| 分 组 | 频数 | 频率 | 频率/组距 |
| [157,161) | |||
| [161,165) | |||
| [165,169) | |||
| [169,173) | |||
| [173,177) | |||
| [177,181) |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com