
题目列表(包括答案和解析)
| 6 |
| 7 |
| 6 |
| 7 |
(03年上海卷理)(14分)
已知数列![]() (n为正整数)是首项是a1,公比为q的等比数列.
(n为正整数)是首项是a1,公比为q的等比数列.
(1)求和:![]()
(2)由(1)的结果归纳概括出关于正整数n的一个结论,并加以证明.
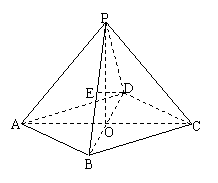
(06年上海卷理)(14分)在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60![]() ,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60
,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60![]() .
.
(1)求四棱锥P-ABCD的体积;
(2)若E是PB的中点,求异面直线DE与PA所成角的大小(结果用反三角函数值表示).
(08年上海卷理)某海域内有一孤岛,岛四周的海平面(视为平面)上有一浅水区(含边界),其边界是长轴长为2a,短轴长为2b的椭圆,已知岛上甲、乙导航灯的海拔高度分别为h1、h2,且两个导航灯在海平面上的投影恰好落在椭圆的两个焦点上,现有船只经过该海域(船只的大小忽略不计),在船上测得甲、乙导航灯的仰角分别为θ1、θ2,那么船只已进入该浅水区的判别条件是 .

(06年上海卷理)(12分)
求函数![]() =2
=2![]() +
+![]() 的值域和最小正周期.
的值域和最小正周期.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com