(2009湖南卷理)设函数在（，+）内有定义。对于给定的正数K，定义函数

取函数=。若对任意的，恒有=，则           

A．K的最大值为2                       B. K的最小值为2

C．K的最大值为1                       D. K的最小值为1                     【　】

（04年湖南卷文）（12分）

已知数列{a_n}是首项为a且公比q不等于1的等比数列，S_n是其前n项的和，a₁,2a₇,3a₄ 成等差数列.

（I）证明  12S₃,S₆,S₁₂-S₆成等比数列；

（II）求和T_n=a₁+2a₄+3a₇+…+na_3n-2.

（湖南卷理3）已知变量x、y满足条件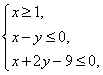则的最大值是(     )

A.2               B.5              C.6                       D.8

(2010年高考湖南卷)在区间[－1，2]上随机取一个数x，则|x|≤1的概率为________．

（08年湖南卷理）对有n(n≥4)个元素的总体进行抽样，先将总体分成两个子总体

和 (m是给定的正整数，且2≤m≤n-2),再从

每个子总体中各随机抽取2个元素组成样本.用表示元素i和j同时出现在样

本中的概率，则=          ; 所有 (1≤i＜j≤的和等于           .