
题目列表(包括答案和解析)
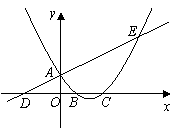
已知:直线![]() 与
与![]() 轴交于A,与
轴交于A,与![]() 轴交于D,抛物线
轴交于D,抛物线![]() 与直线交于A、E两点,与
与直线交于A、E两点,与![]() 轴交于B、C两点,且B点坐标为 (1,0).
轴交于B、C两点,且B点坐标为 (1,0).![]()
(1)求抛物线的解析式;
(2)动点P在![]() 轴上移动,当△PAE是直角三角形时,求点P的坐标.
轴上移动,当△PAE是直角三角形时,求点P的坐标.
(3)在抛物线的对称轴上找一点M,使![]() 的值最大,求出点M的坐标.
的值最大,求出点M的坐标.
已知:如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点A、B,点A的坐标为(4,0)
轴交于点A、B,点A的坐标为(4,0)
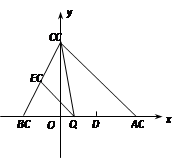
1.求该抛物线的解析式;
2.点Q是线段AB上的动点,过点Q作QE//AC,交BC于点E,连接CQ,设△CQE的面积为S,Q(m,0),试求S与m之间的函数关系式(写出自变量m的取值范围);
3.在(2)的条件下,当△CQE的面积最大时,求点E的坐标.
4.若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0). 问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标,若不存在,请说明理由.
已知:如图,抛物线 与
与 轴交于点
轴交于点 ,与
,与 轴交于点A、B,点A的坐标为(4,0)
轴交于点A、B,点A的坐标为(4,0)

1.求该抛物线的解析式;
2.点Q是线段AB上的动点,过点Q作QE//AC,交BC于点E,连接CQ,设△CQE的面积为S,Q(m,0),试求S与m之间的函数关系式(写出自变量m的取值范围);
3.在(2)的条件下,当△CQE的面积最大时,求点E的坐标.
4.若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0). 问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标,若不存在,请说明理由.
| k2 | x |
 直平分OB,垂足为D,求:
直平分OB,垂足为D,求: 直线y=k1x+b与双曲线y=
直线y=k1x+b与双曲线y=| k2 | x |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com