
题目列表(包括答案和解析)
| 2 |

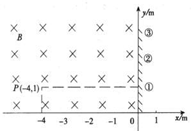 如图所示,在直角坐标系的第二象限内有垂直纸面向里的匀强磁场,磁感应强度的大小为0.1T,在y轴的正半轴上竖有一挡板,板足够长,挡板平面垂直于纸面.在P(-4,1)点有一粒子放射源,能连续地向各个方向放射出速率相同的同种带正电粒子,粒子的质量m=1.0×10ˉ6kg,带电荷量为q=+1×10ˉ5 C,不计粒子重力,求(结果保留两位有效数字):
如图所示,在直角坐标系的第二象限内有垂直纸面向里的匀强磁场,磁感应强度的大小为0.1T,在y轴的正半轴上竖有一挡板,板足够长,挡板平面垂直于纸面.在P(-4,1)点有一粒子放射源,能连续地向各个方向放射出速率相同的同种带正电粒子,粒子的质量m=1.0×10ˉ6kg,带电荷量为q=+1×10ˉ5 C,不计粒子重力,求(结果保留两位有效数字):| 2 |
 )处平行x轴向右运动,并先后通过两个匀强磁场区域.
)处平行x轴向右运动,并先后通过两个匀强磁场区域.
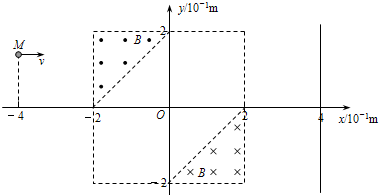
如图所示,在直角坐标系的第二象限和第四象限中的直角三角形区域内,分布着磁感应强度均为B=5.0×10-3 T的匀强磁场,方向分别垂直纸面向外和向里.一质量m=6.4×10-27 kg、电荷量q=+3.2×10-19 C的未知带电粒子(未知带电粒子重力不计),由静止开始经加速电压U=1250 V的电场(图中未画出)加速后,从坐标点M(-4,![]() )处平行x轴向右运动,并先后通过两个匀强磁场区域.
)处平行x轴向右运动,并先后通过两个匀强磁场区域.

(1)求未知带电粒子在磁场中的运动半径.(结果用根式表示)
(2)在图中画出从直线x=-4到直线x=4之间未知带电粒子的运动轨迹,并在图中标明轨迹与直线x=4交点的坐标.
(3)求出未知带电粒子在两个磁场区域偏转所用的时间.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com