
题目列表(包括答案和解析)
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路 ”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
|
|
男性 |
女性 |
合计 |
|
反感 |
10 |
|
|
|
不反感 |
|
8 |
|
|
合计 |
|
|
30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路 ”的路人的概率是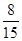 .
.
(Ⅰ)请将上面的列表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路 ”与性别是否有关?(
当 <2.706时,没有充分的证据判定变量性别有关,当
<2.706时,没有充分的证据判定变量性别有关,当
 >2.706时,有90%的把握判定变量性别有关,当
>2.706时,有90%的把握判定变量性别有关,当 >3.841时,有95%的把握判定变量性别有关,当
>3.841时,有95%的把握判定变量性别有关,当
 >6.635时,有99%的把握判定变量性别有关)
>6.635时,有99%的把握判定变量性别有关)
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路 ”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
| | 男性 | 女性 | 合计 |
| 反感 | 10 | | |
| 不反感 | | 8 | |
| 合计 | | | 30 |
 .
.
 <2.706时,没有充分的证据判定变量性别有关,当
<2.706时,没有充分的证据判定变量性别有关,当
 >2.706时,有90%的把握判定变量性别有关,当
>2.706时,有90%的把握判定变量性别有关,当 >3.841时,有95%的把握判定变量性别有关,当
>3.841时,有95%的把握判定变量性别有关,当
 >6.635时,有99%的把握判定变量性别有关)
>6.635时,有99%的把握判定变量性别有关)| | 男性 | 女性 | 合计 |
| 反感 | 10 | | |
| 不反感 | | 8 | |
| 合计 | | | 30 |
 .
.
 <2.706时,没有充分的证据判定变量性别有关,当
<2.706时,没有充分的证据判定变量性别有关,当
 >2.706时,有90%的把握判定变量性别有关,当
>2.706时,有90%的把握判定变量性别有关,当 >3.841时,有95%的把握判定变量性别有关,当
>3.841时,有95%的把握判定变量性别有关,当
 >6.635时,有99%的把握判定变量性别有关)
>6.635时,有99%的把握判定变量性别有关)给出下列几个命题
①从匀速传递的产品生产流水线上,质检员每10分钟从某处抽取一件产品进行某项指标检测,这样的抽样是分层抽样。
②对于一组数据xi(i=1,2,…![]() ),如果将它们变换成xi+1(i=1,2,…,
),如果将它们变换成xi+1(i=1,2,…,![]() ),则变换后的数据平均数变了,而方差保持不变.
),则变换后的数据平均数变了,而方差保持不变.
③在回归直线方程![]() =0.1x+10中,当解释变量x每增加一个单位时,预报变量
=0.1x+10中,当解释变量x每增加一个单位时,预报变量![]() 增加0.1个单位.
增加0.1个单位.
④某地气象局预报:5月9日本地降水概率为90%.结果这天一点雨都没下,这表明天气矛盾并不科学.
⑤如果一个随机变量是众多、互不相干的、不分主次的偶然因素作用结果之和,那么这个随机变量就服从或近似服从正态分布,
其中正确命题的序号为 (把你认为所有正确命题的序号都填上)
(本小题满分12分)袋中装有10个大小相同的小球,其中黑球3个,白球n个(![]() ,其余均为红球;
,其余均为红球;
(1):从袋中一次任取2个球,如果这2个球颜色相同的概率是![]() ,求红球的个数。
,求红球的个数。
(2):在(1)的条件下,从袋中任取2个球,若取一个白球记1分,取一个黑球记2分,取一个红球记3分,用![]() 表示取出的两个球的得分的和;
表示取出的两个球的得分的和;
①求随机变量![]() 的分布列及期望
的分布列及期望![]() 。w.w.^w.k.&s.5*u.c.#om
。w.w.^w.k.&s.5*u.c.#om
②记“关于x的不等式![]() 的解集是实数集R”为事件A,求事件A发生的概率。
的解集是实数集R”为事件A,求事件A发生的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com