
题目列表(包括答案和解析)
函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。
(1)求实数a,b,并确定函数 的解析式;
的解析式;
(2)判断 在(-1,1)上的单调性,并用定义证明你的结论;
在(-1,1)上的单调性,并用定义证明你的结论;
(3)写出 的单调减区间,并判断
的单调减区间,并判断 有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
【解析】本试题主要考查了函数的解析式和奇偶性和单调性的综合运用。第一问中,利用函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。
解得 ,
,
(2)中,利用单调性的定义,作差变形判定可得单调递增函数。
(3)中,由2知,单调减区间为 ,并由此得到当,x=-1时,
,并由此得到当,x=-1时, ,当x=1时,
,当x=1时,
解:(1) 是奇函数,
是奇函数, 。
。
即 ,
, ,
, ………………2分
………………2分
 ,又
,又 ,
, ,
, ,
,
(2)任取 ,且
,且 ,
,
 ,………………6分
,………………6分
 ,
,
 ,
, ,
, ,
, ,
,
 在(-1,1)上是增函数。…………………………………………8分
在(-1,1)上是增函数。…………………………………………8分
(3)单调减区间为 …………………………………………10分
…………………………………………10分
当,x=-1时, ,当x=1时,
,当x=1时, 。
。
P(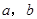 )是平面上的一个点,设事件A表示“
)是平面上的一个点,设事件A表示“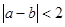 ”,其中
”,其中 为实常数.
为实常数.
(1)若 均为从0,1,2,3,4五个数中任取的一个数,求事件A发生的概率;
均为从0,1,2,3,4五个数中任取的一个数,求事件A发生的概率;
(2)若 均为从区间[0,5)任取的一个数,求事件A发生的概率.
均为从区间[0,5)任取的一个数,求事件A发生的概率.
【解析】本试题考查了几何概型和古典概型结合的一道综合概率计算试题。首先明确区域中的所有基本事件数或者区域表示的面积,然后分别结合概率公式求解得到。
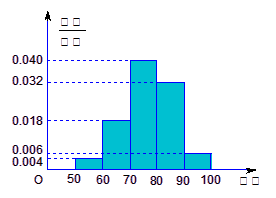 某班50名学生在一次综合测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:每一组
某班50名学生在一次综合测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:每一组![]() ,第二组
,第二组![]() ,……,第五组
,……,第五组![]() .下图是按上述分组方法得到的频率分布直方图.
.下图是按上述分组方法得到的频率分布直方图.
(I)若成绩大于或等于60且小于80,
认为合格,求该班在这次综合测试中
成绩合格的人数;
(II)测试成绩在![]() 内的
内的
学生共有多少人?从这几名同学中随机抽取两名同学,设其测试成绩分别为![]() 、
、![]() ,求事件“
,求事件“![]() ”的概率
”的概率
|
已知集合A={1.3. 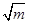 },B={1,m} ,A
},B={1,m} ,A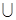 B=A, 则m=
B=A, 则m=
A、0或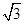 B、0或3 C、1或
B、0或3 C、1或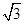 D、1或3
D、1或3
【解析】因为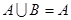 ,所以
,所以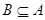 ,所以
,所以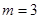 或
或 .若
.若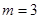 ,则
,则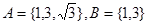 ,满足
,满足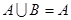 .若
.若 ,解得
,解得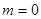 或
或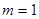 .若
.若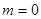 ,则
,则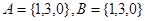 ,满足
,满足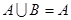 .若
.若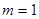 ,
,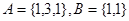 显然不成立,综上
显然不成立,综上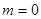 或
或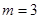 ,选B.
,选B.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com