
题目列表(包括答案和解析)
 操作与探索:如图,在△ABC中,AC=BC=2,∠C=90°,将一块三角板的直角顶点放在斜边的中点P处,绕点P旋转.设三角板的直角边PM交线段CB于E点,当CE=0,即E点和C点重合时,有PE=PB,△PBE为等腰三角形,此外,当CE等于
操作与探索:如图,在△ABC中,AC=BC=2,∠C=90°,将一块三角板的直角顶点放在斜边的中点P处,绕点P旋转.设三角板的直角边PM交线段CB于E点,当CE=0,即E点和C点重合时,有PE=PB,△PBE为等腰三角形,此外,当CE等于
| 3 | 2 |

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
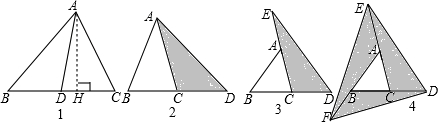
操作与探索:
已知点O为直线AB上一点,作射线OC,将直角三角板ODE放置在直线上方(如图①),使直角顶点与点O重合,一条直角边OD重叠在射线OA上,将三角板绕点O旋转

(1)当三角板旋转到如图②的位置时,若OD平分∠AOC,试说明OE也平分∠BOC.
(2)若OC⊥AB,垂足为点O(如图③),请直接写出与∠DOB互补的角
(3)若∠AOC=135°(如图④),三角板绕点O按顺时针从如图①的位置开始旋转,到OE边与射线OB重合结束. 请通过操作,探索:在旋转过程中,∠DOB ∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.
∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.
操作与探索:
已知点O为直线AB上一点,作射线OC,将直角三角板ODE放置在直线上方(如图①),使直角顶点与点O重合,一条直角边OD重叠在射线OA上,将三角板绕点O旋转
(1)当三角板旋转到如图②的位置时,若OD平分∠AOC,试说明OE也平分∠BOC.
(2)若OC⊥AB,垂足为点O(如图③),请直接写出与∠DOB互补的角
(3)若∠AOC=135°(如图④),三角板绕点O按顺时针从如图①的位置开始旋转,到OE边与射线OB重合结束. 请通过操作,探索:在旋转过程中,∠DOB ∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.
∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com