（03年江苏卷）（12分）当物体从高空下落时，空气阻力随速度的增大而增大，因此经过一段距离后将匀速下落，这个速度称为此物体下落的终极速度。已知球形物体速度不大时所受的空气阻力正比于速度v且正比于球半径r，即阻力f=krv，k是比例系数。对于常温下的空气，比例系数k=3.4×10^-4Ns/m²。已知水的密度ρ=1.0×10³kg/m³，取重力加速度g=10m/s²。试求半径r=0.10mm的球形雨滴在无风情况下的终极速度v_r。（结果取两位数字）

（06年江苏卷）我省沙河抽水蓄能电站自2003年投入运行以来，在缓冲用电高峰电力紧方面，取得良好的社会效益和经济效益，抽水蓄能电站的工作原理是，在用电低谷时（如深夜），电站利用电网多余电能把水抽到高处蓄水池中，到用电高峰时，再利用蓄水池中的水发电，如图蓄水池（上游水库）可视为长方体，有效总库容量（可用于发电）为V，蓄水后水位高出下游水面H，发电过程中上游水库水位最大落差为d，统计资料表明，该电站利用抽水用电为2.4×10⁸kw?h，发电量1.8×10⁸kw?h，则下列计算结果正确的是（水的密度为ρ，重力加速度为g，涉及重力势能的计算均以下游水面为零势能面）（    ）

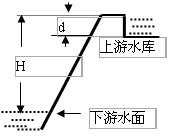
A.能用于发电的水的最大重力势能E_P=ρvgH

B.能用于发电的水的最大重力势能E_P=ρvg()

C.电站的总效率达75%

D.该电站平均每天所发电能可供给一个大城市居民用电（电功率以10⁵kw计）约10h

（09年北京卷23）．单位时间内流过管道横截面的液体体积叫做液体的体积流量（以下简称流量）。由一种利用电磁原理测量非磁性导电液体（如自来水、啤酒等）流量的装置，称为电磁流量计。它主要由将流量转换为电压信号的传感器和显示仪表两部分组成。

传感器的结构如图所示，圆筒形测量管内壁绝缘，其上装有一对电极和c,a,c间的距离等于测量管内径D，测量管的轴线与a、c的连接放像以及通过电线圈产生的磁场方向三者相互垂直。当导电液体流过测量管时，在电极a、c的间出现感应电动势E，并通过与电极连接的仪表显示出液体流量Q。设磁场均匀恒定，磁感应强度为B。

（1）已知，设液体在测量管内各处流速相同，试求E的大小（去3.0）

（2）一新建供水站安装了电磁流量计，在向外供水时流量本应显示为正值。但实际显示却为负值。经检查，原因是误将测量管接反了，既液体由测量管出水口流入，从如水口流出。因为已加压充满管道。不便再将测量管拆下重装，请你提出使显示仪表的流量指示变为正直的简便方法；

（3）显示仪表相当于传感器的负载电阻，其阻值记为 a、c间导电液体的电阻r随液体电阻率色变化而变化，从而会影响显示仪表的示数。试以E、R。r为参量，给出电极a、c间输出电压U的表达式，并说明怎样可以降低液体电阻率变化对显示仪表示数的影响。

（09年江苏二十所名校联考）（14分）如图甲所示，空间存在竖直向下的磁感应强度为0.6T的匀强磁场，MN、PQ是相互平行的、处于同一水平面内的长直导轨（电阻不计），导轨间距为0.2m，连在导轨一端的电阻为R。导体棒ab的电阻为0.1Ω，质量为0.3kg，跨接在导轨上，与导轨间的动摩擦因数为0.1。从零时刻开始，通过一小型电动机对ab棒施加一个牵引力F，方向水平向左，使其从静止开始沿导轨做加速运动，此过程中棒始终保持与导轨垂直且接触良好。图乙是棒的速度--时间图像，其中OA段是直线，AC是曲线，DE是曲线图像的渐近线，小型电动机在10s末达到额定功率，此后功率保持不变。g取10 m/s²。求：

（1）在0--18s内导体棒获得加速度的最大值；

（2）电阻R的阻值和小型电动机的额定功率；

（3）若已知0--10s内R上产生的热量为3.1J，则此过程中牵引力做的功为多少?

（03年江苏卷）（13分）（1）如图1，在光滑水平长直轨道上，放着一个静止的弹簧振子，它由一轻弹簧两端各联结一个小球构成，两小球质量相等。现突然给左端小球一个向右的速度u₀，求弹簧第一次恢复到自然长度时，每个小球的速度。

（2）如图2，将N个这样的振子放在该轨道上。最左边的振子1被压缩至弹簧为某一长度后锁定，静止在适当位置上，这时它的弹性势能为E₀。其余各振子间都有一定的距离。现解除对振子1的锁定，任其自由运动，当它第一次恢复到自然长度时，刚好与振子2碰撞，此后，继续发生一系列碰撞，每个振子被碰后刚好都是在弹簧第一次恢复到自然长度时与下一个振子相碰。求所有可能的碰撞都发生后，每个振子弹性势能的最大值。已知本题中两球发生碰撞时，速度交换，即一球碰后的速度等于另一球碰前的速度。