练习册

  • 练习册
  • 试题
    证明三角等式的思路和方法. (1)思路:利用三角公式进行化名.化角.改变运算结构.使等式两边化为同一形式. (2)证明方法:综合法.分析法.比较法.代换法.相消法.数学归纳法. 【查看更多】

     

    题目列表(包括答案和解析)

    应用数学归纳法证明“”，当n=1时，等式的左边和右边分别是（　）

    A．1，　　　　　　　　　　　　  B．

    C．　　　　　　   D．1，

    查看答案和解析>>

    用数不归纳法证明

    ，在验证n=1时，等式的左边和右边应分别是

    [　　]

    A．1，1
    B．，
    C．1，
    D．，

    查看答案和解析>>

    应用数学归纳法证明“”，当n=1时，等式的左边和右边分别是（　）

    A．1，　　　　　　　　　　　　  B．

    C．　　　　　　   D．1，

    查看答案和解析>>

    在学习二项式定理时，我们知道杨辉三角中的数具有两个性质：①每一行中的二项式系数是“对称”的，即第1项与最后一项的二项式系数相等，第2项与倒数第2项的二项式系数相等，…；②图中每行两端都是1，而且除1以外的每一个数都等于它肩上两个数的和．我们也知道，性质①对应于组合数的一个性质：cnm=Cnn-m．
    （1）试写出性质②所对应的组合数的另一个性质；
    （2）请利用组合数的计算公式对（1）中组合数的另一个性质作出证明．

    查看答案和解析>>

    （本小题满分14分）

    观察下列三个三角恒等式

    （1）

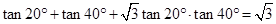
    （2）

    （3）

    的特点，由此归纳出一个一般的等式，使得上述三式为它的一个特例，并证明你的结论

    （说明：本题依据你得到的等式的深刻性分层评分．）

     

    查看答案和解析>>


    同步练习册答案