练习册

  • 练习册
  • 试题
    15．已知函数f1(x)＝3|x-p1|.f2(x)＝2·3|x-p2|(x∈R.p1.p2为常数).函数f(x)定义为:对每个给定的实数x.f(x)＝ (1)求f(x)＝f1(x)对所有实数x成立的充分必要条件(用p1.p2表示), (2)设a.b是两个实数.满足a<b.且p1.p2∈(a.b)．若f(a)＝f(b).求证:函数f(x)在区间[a.b]上的单调增区间的长度之和为(闭区间[m.n]的长度定义为n-m)． 解:(1)由f(x)的定义可知. f(x)＝f1(x)(对所有实数x) 等价于f1(x)≤f2(x)(对所有实数x). 这又等价于3|x-p1|≤2·3|x-p2|. 即3|x-p1|-|x-p2|≤2对所有实数x均成立．(*) 易知函数|x-p1|-|x-p2|(x∈R)的最大值为|p2-p1|.故(*)等价于3|p2-p1|≤2.即|p2-p1|≤log32.这就是所求的充分必要条件． (2)分两种情形讨论． (ⅰ)当|p1-p2|≤log32时.由(1)知f(x)＝f1(x)(对所有实数x∈[a.b]).则由f(a)＝f(b)及a<p1<b易知p1＝.再由f1(x)＝的单调性可知.f(x)在区间[a.b]上的单调增区间的长度为b-＝.如下图． (ⅱ)当|p1-p2|>log32时. 不妨设p1<p2.则p2-p1>log32. 于是.当x≤p1时. 有f1(x)=3p1-x<3p2-x<f2(x). 从而f(x)=f1(x)． 当x≥p2时.f1(x)=3x-p1=3p2-p1·3x-p2>3log32·3x-p2=f2(x).从而f(x)=f2(x)． 当p1<x<p2时.f1(x)=3x-p1及f2(x)=2·3p2-x. 由方程3x0-p1=2·3p2-x0.解得f1(x)与f2(x)图象交点的横坐标为 显然p1<x0＝P2-[(p2-p1)-log32]<p2.这表明x0在p1与p2之间． 由①易知f(x)＝ 综上可知.在区间[a.b]上. f(x)＝ 如下图所示． 【查看更多】

     

    题目列表(包括答案和解析)

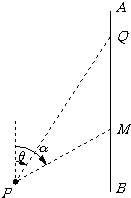    （2008•江苏二模）如图，AB是沿太湖南北方向道路，P为太湖中观光岛屿，Q为停车场，PQ=5.2km．某旅游团游览完岛屿后，乘游船回停车场Q，已知游船以13km/h的速度沿方位角θ的方向行驶，sinθ=
    5
    13
    ．游船离开观光岛屿3分钟后，因事耽搁没有来得及登上游船的游客甲为了及时赶到停车地点Q与旅游团会合，立即决定租用小船先到达湖滨大道M处，然后乘出租汽车到点Q（设游客甲到达湖滨大道后能立即乘到出租车）．假设游客甲乘小船行驶的方位角是α，出租汽车的速度为66km/h．
    （Ⅰ）设sinα=
    4
    5
    ，问小船的速度为多少km/h时，游客甲才能和游船同时到达点Q；
    （Ⅱ）设小船速度为10km/h，请你替该游客设计小船行驶的方位角α，当角α余弦值的大小是多少时，游客甲能按计划以最短时间到达Q．

    查看答案和解析>>

    （2008•江苏二模）在△ABC中，已知
    AB
    =（-1，2），
    AC
    =（2，1），则△ABC的面积等于
    5
    2
    5
    2
    ．

    查看答案和解析>>

    （2008江苏）如图，在平面直角坐标系中，以轴为始边做两个锐角，它们的终边分别与单位圆相交于A，B两点，已知A，B的横坐标分别为

    （1）       求的值；   （2） 求的值。

    查看答案和解析>>


    同步练习册答案