
题目列表(包括答案和解析)
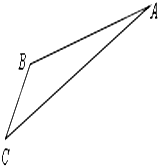 如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客同时从A处下山,甲沿AC匀速步行,速度为50m/min.乙从A乘缆车到B,在B处停留1min后,再匀速步行到C.假设缆车匀速直线运动的速度为130m/min,山路AC长为1260m,经测量,cosA=
如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客同时从A处下山,甲沿AC匀速步行,速度为50m/min.乙从A乘缆车到B,在B处停留1min后,再匀速步行到C.假设缆车匀速直线运动的速度为130m/min,山路AC长为1260m,经测量,cosA=| 12 |
| 13 |
| 3 |
| 5 |
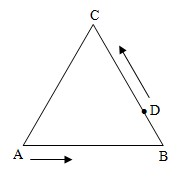 例2:如图:△ABC是边长为3厘米的正三角形,D是BC边上靠近点B的三等分点,甲、乙两个质点分别从点A、D同时出发,都以1厘米/秒的速度按图示方向沿三角形的边作匀速运动,经过时间t(0≤t≤3)秒后,两质点的距离为S(t).
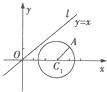
例2:如图:△ABC是边长为3厘米的正三角形,D是BC边上靠近点B的三等分点,甲、乙两个质点分别从点A、D同时出发,都以1厘米/秒的速度按图示方向沿三角形的边作匀速运动,经过时间t(0≤t≤3)秒后,两质点的距离为S(t). (2012•江西)如图,|OA|=2(单位:m),OB=1(单位:m),OA与OB的夹角为
(2012•江西)如图,|OA|=2(单位:m),OB=1(单位:m),OA与OB的夹角为| π |
| 6 |
 |
| BDC |
 |
| BDC |
 直线x+
直线x+| 3 |
| 2 |
 设有半径为3km的圆形村落,A、B两人同时从村落中心出发.B一直向北直行;A先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝B所在的方向前进.
设有半径为3km的圆形村落,A、B两人同时从村落中心出发.B一直向北直行;A先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝B所在的方向前进.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com