(12分)如图14所示，回旋加速器D形盒的半径为R，用来加速质量为m、电荷量为q的质子，使质子由静止加速到能量为E后，由A孔射出，求：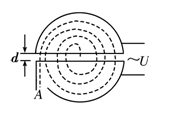

(1)加速器中匀强磁场B的方向和大小；
(2)设两D形盒间距为d，其间电压为U，电场视为匀强电场，质子每次经电
场加速后能量增加，加速到上述能量所需回旋周数；
(3)加速到上述能量所需时间．

(12分)如图14所示，回旋加速器D形盒的半径为R，用来加速质量为m、电荷量为q的质子，使质子由静止加速到能量为E后，由A孔射出，求：

(1)加速器中匀强磁场B的方向和大小；

(2)设两D形盒间距为d，其间电压为U，电场视为匀强电场，质子每次经电

场加速后能量增加，加速到上述能量所需回旋周数；

(3)加速到上述能量所需时间．

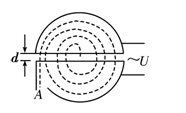
1932年，劳伦斯和利文斯设计出了回旋加速器。回旋加速器的工作原理如图14（甲）所示，它由两个铝制D型金属扁盒组成，两个D形盒正中间开有一条狭缝；两个D型盒处在匀强磁场中并接有高频交变电压。图14（乙）为俯视图，在D型盒上半面中心S处有一正粒子源，它发出的带电粒子，经狭缝电压加速后，进入D型盒中，在磁场力的作用下运动半周，再经狭缝电压加速；为保证粒子每次经过狭缝都被加速，应设法使交变电压的周期与粒子在狭缝及磁场中运动的周期一致。如此周而复始，最后到达D型盒的边缘，获得最大速度后射出。

置于高真空中的D形金属盒的最大轨道半径为R，两盒间的狭缝很小，带电粒子穿过的时间可以忽略不计。粒子源S射出的是质子流，初速度不计，D形盒的交流电压为U，静止质子经电场加速后，进入D形盒，磁场的磁感应强度B，质子的质量为m，电量为q，求：

（1）质子最初进入D形盒的动能多大？

（2）质子经回旋加速器最后得到的动能多大？

（3）要使质子每次经过电场都被加速，则加交流电源的周期是多少？