练习册

  • 练习册
  • 试题
    解决集合问题.首先要弄清楚集合中的元素是什么.即元素分析法的掌握． 弄清集合中元素的本质属性.能化简的要化简, 抓住集合中元素的个性质.对互异性要注意检验, 正确进行“集合语言 和普通“数学语言 的相互转化． 【查看更多】

     

    题目列表(包括答案和解析)

    乒乓球比赛规则规定，一局比赛，双方比分在10平前，一方连续发球2次后，对方再连续发球2次，依次轮换，每次发球，胜方得1分，负方得0分。设在甲、乙的比赛中，每次发球，发球1分的概率为0.6，各次发球的胜负结果相互独立。甲、乙的一局比赛中，甲先发球。

    （I）     求开球第4次发球时，甲、乙的比分为1比2的概率；

    （II）   求开始第5次发球时，甲得分领先的概率。

    【解析】本试题主要是考查了关于独立事件的概率的求解，以及分布列和期望值问题。首先要理解发球的具体情况，然后对于事件的情况分析，讨论，并结合独立事件的概率求解结论。

    【点评】首先从试题的选材上来源于生活，同学们比较熟悉的背景，同时建立在该基础上求解进行分类讨论的思想的运用，以及能结合独立事件的概率公式求解分布列的问题。情景比较亲切，容易入手，但是在讨论情况的时候，容易丢情况。

     

    查看答案和解析>>

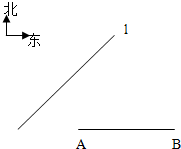    如图，某开发区旁边有一条东北走向的公路l，开发区内有两工厂A，B（B在A正东4km），A工厂到公路l的距离为(
    		6
    -
    		2
    )km    ．建立适当的坐标系，解决下列问题：
    （Ⅰ）求公路l所在直线的方程；
    （Ⅱ）在公路l上有一站点M到A，B两工厂路程之和最小，现要建一条经过M的环行公路，使公路上每一点到A，B两工厂路程之和相等，求环行公路所在曲线的方程；
    （Ⅲ）开发区内有一物资储藏库C位于B工厂西北距B工厂
    		2
    km    ，在（Ⅱ）中的环行公路上设一站点N，使站点N到C，B两地的距离之和最小．试问：满足要求的点N在什么位置（不要证明），并求|NC|+|NB|的值．

    查看答案和解析>>

    （2008•奉贤区模拟）我们将具有下列性质的所有函数组成集合M：函数y=f（x）（x∈D），对任意x，y，
    x+y
    2
    ∈D    均满足f(
    x+y
    2
    )≥
    1
    2
    [f(x)+f(y)]    ，当且仅当x=y时等号成立．
    （1）若定义在（0，+∞）上的函数f（x）∈M，试比较f（3）+f（5）与2f（4）大小．
    （2）给定两个函数：f1(x)=
    1
    x
    (x＞0)    ，f2（x）=logax（a＞1，x＞0）．证明：f1（x）∉M，f2（x）∈M．
    （3）试利用（2）的结论解决下列问题：若实数m、n满足2m+2n=1，求m+n的最大值．

    查看答案和解析>>

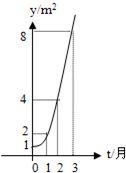    20、如图所示的是某池塘中的浮萍蔓延的面积y（m2）与时间t（月）的关系：y=at，请解决以下问题：
    ①求出这个指数函数的表达式；
    ②求第5个月时浮萍的面积； 
    ③浮萍从4m2蔓延到16m2恰好要经过多少个月．

    查看答案和解析>>

    （2008•奉贤区一模）我们将具有下列性质的所有函数组成集合M：函数y=f（x）（x∈D），对任意x，y，
    x+y
    2
    ∈D    均满足f(
    x+y
    2
    )≥
    1
    2
    [f(x)+f(y)]    ，当且仅当x=y时等号成立．
    （1）若定义在（0，+∞）上的函数f（x）∈M，试比较f（3）+f（5）与2f（4）大小．
    （2）设函数g（x）=-x2，求证：g（x）∈M．
    （3）已知函数f（x）=log2x∈M．试利用此结论解决下列问题：若实数m、n满足2m+2n=1，求m+n的最大值．

    查看答案和解析>>


    同步练习册答案