查看答案和解析>>

已知f(x)是定义在R上的偶函数，且x≥0时，。
（1）求f(0)，f(-1)；
（2）求函数f(x)的表达式；
（3）若f(a-1)-f(3-a)＜0，求a的取值范围。

查看答案和解析>>

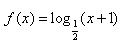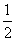已知f（x）=ax²+2x，g（x）=lnx，
(1)求函数y=xg（x）-2x的单调区间；
(2)如果y=f（x）在[1，+∞)上是增函数，求a的取值范围；
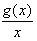(3)是否存在a＞0，使方程=f′（x）-（2a+1）在区间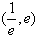内有且只有两个不相等的实数根，若存在求出a的取值范围，不存在说明理由。

查看答案和解析>>

已知f（x）是定义在[-1，1]上的奇函数，且f（1）=1，若a，b∈[-1，1]，a+b≠0时，都有。
（1）证明：函数f（x）在[-1，1]上是增函数；
（2）解不等式：；
（3）若f（x）≤m²-2pm+1对所有x∈[-1，1]，任意p∈[-1，1]恒成立，求实数m的取值范围。

查看答案和解析>>

查看答案和解析>>

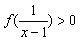必修

一、填空题

1、8  2、  3、2|P|  4、  5、向左移，在把各点的横坐标伸长到原来的3倍

6、18  7、120度  8、  9、  10、②④  11、  12、  13、  14、

二、解答题

15．解：（Ⅰ）＝．………… 4分

由，得．

∴函数的单调增区间为 ．………… 7分

（Ⅱ）由，得．

∴．            ………………………………………… 10分

∴，或，

即或． 

∵，∴．     …………………………………………… 14分

16．解：（Ⅰ）n≥2时，．     ………………… 4分

n＝1时，，适合上式，

∴．               ………………… 5分

（Ⅱ），．          ………………… 8分

即．

∴数列是首项为4、公比为2的等比数列．   ………………… 10分

，∴．……………… 12分

T_n＝＝．            ………………… 14分

17、⑴    ⑵        ⑶不能

18、⑴

⑵=1时，的最大值为20200，=10时，的最小值为12100。

19、⑴易知AB恒过椭圆的右焦点F（，0）    ⑵ S=       ⑶存在。

20、⑴

⑵或

⑶（，）

附加题选修参考答案

1、⑴BB=  ， ⑵  

2、⑴    ⑵  ，，  ，EX=1

3、   

4、⑴    ⑵ MN=2 

5、⑴特征值为2和3 ，对应的特征向量分别为及，

⑵ ，椭圆在矩阵的作用下对应得新方程为

6、提示：，然后用基本不等式或柯西不等式即可。