
题目列表(包括答案和解析)
|
|
(本小题满分12分)
已知平面向量a=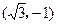 ,b=
,b=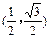
(1)证明a b;
b;
(2)若存在实数k,t,使x=a+ b,y=-ka+tb,且x
b,y=-ka+tb,且x y,试求k,t的函数关系式
y,试求k,t的函数关系式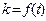 ;
;
(3)根据(2)的结论,讨论关于t的方程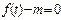 的解的情况。
的解的情况。
(本小题满分12分)
若平面向量 (
(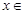 R),函数
R),函数 .
.
(1)求函数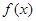 的值域;
的值域;
(2)记△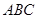 的内角
的内角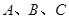 的对边长分别为
的对边长分别为 ,若
,若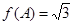 ,且
,且
 ,求角
,求角 的值.
的值.
(本小题满分12分)
设平面向量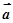 =
( m , -1),
=
( m , -1), 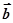 =
( 2 , n ),其中 m, n
=
( 2 , n ),其中 m, n 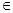 {-2,-1,1,2}.
{-2,-1,1,2}.
(1)记“使得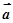 //
//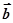 成立的(
m,n )”为事件A,求事件A发生的概率;
成立的(
m,n )”为事件A,求事件A发生的概率;
(2)记“使得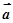 ⊥(
⊥(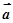 -2
-2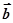 )成立的(
m,n )”为事件B,求事件B发生的概率.
)成立的(
m,n )”为事件B,求事件B发生的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com