下列叙述中正确的是（   ）

①反证法原理是在假设下，如果推出一个矛盾，就证明不成立.

②独立性检验原理是在假设下，如果出现一个与相矛盾的小概率事件，就推断不成立，且该推断犯错误的概率不超过这个小概率.

③三段论可以表示为：大前提：M是P.小前提：S是M.结  论：S是P.

④流程图常常用来表示一些动态过程，通常会有一个 “起点”，一个或多个“终点”.程序框图是流程图的一种.

A．①②③            B．①②④           C．②③④           D．①②③④

 

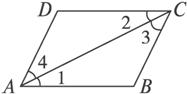
已知，如图，AB是⊙O的直径，AC切⊙O于点A，AC=AB，CO交⊙O于点P，CO的延长线交⊙O于点F，   BP的延长线交AC于点E.

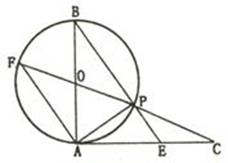
⑴求证：FA∥BE；

⑵求证：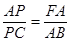

【解析】本试题主要是考查了平面几何中圆与三角形的综合运用。

（1）要证明线线平行，主要是通过证明线线平行的判定定理得到

（2）利用三角形△APC∽△FAC相似，来得到线段成比列的结论。

证明：（1）在⊙O中，∵直径AB与FP交于点O ∴OA=OF

 ∴∠OAF=∠F  ∵∠B=∠F  ∴∠OAF=∠B ∴FA∥BE

（2）∵AC为⊙O的切线，PA是弦  ∴∠PAC=∠F

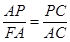
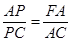∵∠C=∠C ∴△APC∽△FAC  ∴

∴ ∵AB=AC  ∴

 

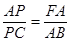
已知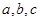是全不相等的正实数，证明：.

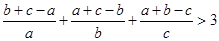【解析】本试题主要考查了不等式的证明，利用分析法和综合法结合来证明。

 

在四边形ABCD中,AB=CD,BC=AD(如图).求证:ABCD为平行四边形.写出三段论形式的演绎推理.

分析：原题可用符号表示为(AB=CD)且(BC=AD)ABCD.

    用演绎推理来证明论题的方法,也就是从包含在论据中的一般原理推出包含在此题中的个别特殊事实.

    为了证明这个命题为真,我们只需在假设前提(AB=CD且BC=AD)为真的情况下,以已知公理、已知定义、已知定理为依据,根据推理规则,导出结论ABCD为真.

一剪刀剪出一条正弦曲线.

把一张纸卷到圆柱形的纸筒面上，卷上几圈.用剪刀斜着将纸筒剪断，再把卷着的纸展开，你就会看到：纸的边缘线是一条波浪形的曲线.

    你知道吗？这条曲线就是正弦曲线！请你来证明这一事实.