练习册

  • 练习册
  • 试题
    三角 三角包括两部分内容:三角函数和两角和与差的三角函数.三角函数主要考查三角函数的性质.图象变换.求函数解析式.最小正周期等. 两角和与差的三角函数中公式较多.应在掌握这些公式的内在联系及推导过程的基础上.理解并熟悉这些公式.特别注意以下几个问题: (1)和.差.倍.半角公式都是用单角的三角函数表示复角的三角函数.这就决定了这些公式应用的广泛性.即这些公式可以将三角函数统一成单角的三角函数. (2)了解公式中角的取值范围.凡使公式中某个三角函数或某个式子失去意义的角.都不适合公式.例如: ()类似还有一些.请自己注意. (3)半角公式中的无理表达式前面的符号取舍.由公式左端的三角函数中角的范围决定.半角正切公式的有理表达式中.无需选择符合.但与的符合是一致的. (4)掌握公式的正用.反用.变形用及在特定条件下用.它可以提高思维起点.缩短思维线路.从而使运算流畅自然.例如: =,, ,. (5)三角函数式的化简与求值.这是中学数学中重要内容之一.并且与解三角形相集合.有的还与复数的三角形式运算相联系.因此须注意常用方法和技巧:切割化弦.升降幂.和积互化.“1 的互化.辅助元素法等. 【查看更多】

     

    题目列表(包括答案和解析)

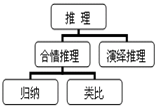    如图是《推理》知识结构框图，根据该框图可得  
    （1）“推理”主要包括两部分内容
    （2）知道“推理”概念后，只能进行“合情推理”内容的学习
    （3）“归纳”与“类比”都不是演绎推理
    （4）可以先学习“类比”再学习“归纳”
    这些命题（　　）

    查看答案和解析>>

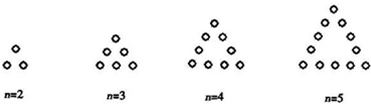    如下图所示，由若干个点组成形如三角形的图形，每条边（包括两个端点）有n（n＞1，n∈N）个点，每个图形总的点数记为an，则
    9
    a2a3
    +
    9
    a3a4
    +
    9
    a4a5
    +…+
    9
    a2010a2011
    =（　　）

    查看答案和解析>>

    已知点P是线段AB上的动点（不包括两端点），点O是线段AB所在直线外一点，若
    OP
    =x
    OA
    +2y
    OB
    （x，y∈R），则
    2
    x
    +
    1
    y
    的最小值是（　　）

    查看答案和解析>>

    （2012•香洲区模拟）如图所示，将若干个点摆成三角形图案，每条边（包括两个端点）有n（n＞1，n∈N*）个点，相应的图案中总的点数记为an，则
    9
    a2a3
    +
    9
    a3a4
    +
    9
    a4a5
    +…+
    9
    a2012a2013
    =（　　）

    查看答案和解析>>

    如图所示，4×3的矩形(每个小方格都是单位正方形)，在起点和终点都在小方格的顶点处的向量中，试问：

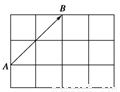
    (1)与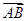相等的向量共有几个；

    (2)与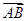平行且模为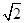的向量共有几个？

    (3)与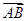方向相同且模为3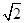的向量共有几个？

    [分析]　非零向量平行(共线)包括两种情况：一种是方向相同，另一种是方向相反．

     

    查看答案和解析>>


    同步练习册答案