
题目列表(包括答案和解析)
改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村 到
到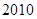 年十年间每年考入大学的人数.为方便计算,
年十年间每年考入大学的人数.为方便计算, 年编号为
年编号为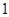 ,
,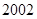 年编号为
年编号为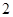 ,…,
,…,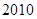 年编号为
年编号为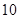 .数据如下:
.数据如下:
|
年份( |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
人数( |
3 |
5 |
8 |
11 |
13 |
14 |
17 |
22 |
30 |
31 |
(1)从这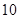 年中随机抽取两年,求考入大学的人数至少有
年中随机抽取两年,求考入大学的人数至少有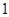 年多于
年多于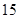 人的概率;
人的概率;
(2)根据前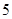 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出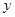 关于
关于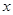 的回归方程
的回归方程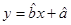 ,并计算第
,并计算第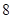 年的估计值和实际值之间的差的绝对值。
年的估计值和实际值之间的差的绝对值。
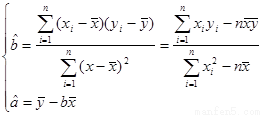
【解析】(1)设考入大学人数至少有1年多于15人的事件为A则P(A)=1-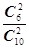 =
=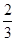 (4’)
(4’)
(2)由已知数据得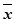 =3,
=3,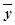 =8,
=8,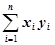 =3+10+24+44+65=146
=3+10+24+44+65=146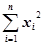 =1+4+9+16+25=55(7’)
=1+4+9+16+25=55(7’)
则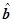 =
=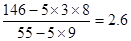 ,
,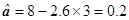 (9’)
(9’)
则回归直线方程为y=2.6x+0.2 (10’)
则第8年的估计值和真实值之间的差的绝对值为
继萨凯里之后,大概又过了半个世纪.欧洲“数学之王”高斯的至友匈牙利数学家伏尔夫刚·鲍里埃,终身从事证明“第五公设”的研究,由于心血耗尽,毫无成效,便怀着沉重的心情,给那酷爱数学的儿子亚诺什·鲍耶(1802~1860)写信,希望小鲍耶“不要再做克服平行公理的尝试”.他忠告儿子说:“投身于这一贪得无度地吞人们的智慧、精力和心血的无底洞,白花时间在上面,一辈子也证不出这个命题来.”他满腹心酸地写到:“我经过了这个毫无希望的夜的黑暗,我在这里面埋没了人生的一切亮光、一切欢乐和一切希望.”最后告诫自己心爱的儿子说:“若再痴恋这一无止无休的劳作,必然会剥夺你生活的一切时间、健康、休息和幸福!”但是,年仅21岁的小鲍耶却是敢向“无底洞”觅求真知的探索者.他认真吸取前人失败的教训,初出茅庐就大显身手.小鲍耶匠心独运,大胆创新,决然将“第五公设”换成他自身的否定.从“三角形三个内角和小于180°”这一令人瞠目结舌的假设出发,建立起一套完整协调、天衣无缝的新几何体系.小鲍耶满怀激情地将自己的科学创见向父亲报捷.老伏尔夫刚以之见教于至友高斯,不久,高斯复信鲍里埃,信中写到:“如果我一开始便说我不能称赞这样的成果,你一定会感到惊讶.但是,我不能不这样说,因为称赞这些成果就等于称赞我自己.令郎的这些工作,他走过的路,以及所获得的成果,跟我过去30年至35年前的所思所得几乎一模一样.”高斯在回信结尾还开诚布公地提到:“我自己的著作,尽管写好的只是一部分,我本来也想发表,因为我怕引某些人的喊声,现在,有了朋友的儿子能够这样写下来,免得他与我一样湮没,那是使我非常高兴的.”这位当代数学大师恐怕做梦也没想到,他这封推心置腹的信,竟会一举撞毁初露锋芒的数坛新星!
高斯的复信给小鲍耶带来意想不到的毁灭性打击.踌躇满志的鲍耶误认为高斯动用自己拥有的崇高权威来垄断和夺取这一新体系的发明优先权.为此,他痛心疾首,认为自己心血浇灌出来的成果和呕心沥血的辛勤工作,竟得不到大家的理解、支持和同情.于是郁郁寡欢,大失所望,发誓抛弃了一切数学研究.
1.对于“数学之王”高斯给鲍耶的回信,你有什么看法呢?如果你是高斯,你该怎样回信?
2.踌躇满志的鲍耶误认为“高斯动用自己拥有的崇高权威来垄断和夺取这一新体系的发明优先权”,进而“郁郁寡欢,大失所望,发誓抛弃了一切数学研究”.你又有何看法呢?假如你是鲍耶,你又该怎么做呢?
| 年份(x) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数(y) | 3 | 5 | 8 | 11 | 13 | 14 | 17 | 22 | 30 | 31 |
 |
| b |
 |
| a |
|
| 年份(x) | 1 | 2 | 3 | 4 | 5 |
| 人数(y) | 3 | 5 | 8 | 11 | 13 |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| |||||||
|
 |
| a |
. |
| y |
. |
| x |
| 年份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数y | 3 | 5 | 8 | 11 | 13 | 14 | 17 | 22 | 30 | 31 |
| ? |
| b |
| ? |
| a |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com