
题目列表(包括答案和解析)
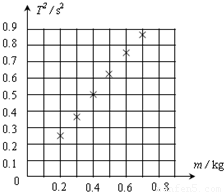
 某同学想“探究影响弹簧振子周期的因素”,以下是他探究弹簧振子的周期T与振子质量m关系的实验.取一根轻弹簧,上端固定在铁架台上,下端系一金属小球,让小球在竖直方向离开平衡位置(在弹性限度范围内)放手后,小球在竖直方向做简谐运动(此装置也称为竖直弹簧振子),他在只改变小球质量的情况下,多次换上不同质量的小球,测得六组比较理想的周期T与小球质量m的数据,并标在以m为横坐标,T2为纵坐标的坐标纸上,即图中用“×”表示的点.请你协助他完成以下几个问题:
某同学想“探究影响弹簧振子周期的因素”,以下是他探究弹簧振子的周期T与振子质量m关系的实验.取一根轻弹簧,上端固定在铁架台上,下端系一金属小球,让小球在竖直方向离开平衡位置(在弹性限度范围内)放手后,小球在竖直方向做简谐运动(此装置也称为竖直弹簧振子),他在只改变小球质量的情况下,多次换上不同质量的小球,测得六组比较理想的周期T与小球质量m的数据,并标在以m为横坐标,T2为纵坐标的坐标纸上,即图中用“×”表示的点.请你协助他完成以下几个问题:| bm |
| bm |
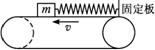
 一皮带传动装置如图所示,皮带的速度v足够大.一根质量不计、劲度系数为k的弹簧一端固定,另一端连接一个质量为m的滑块,已知滑块与皮带间的动摩擦因数为μ.当滑块放到皮带上时,弹簧的轴线恰好水平,若滑块放到皮带上的瞬间,滑块的速度为零,且弹簧正好处于自由长度,则当弹簧第一次伸长到最大时,滑块与皮带间所产生的热量是多少?(已知弹簧振子周期T=2π
一皮带传动装置如图所示,皮带的速度v足够大.一根质量不计、劲度系数为k的弹簧一端固定,另一端连接一个质量为m的滑块,已知滑块与皮带间的动摩擦因数为μ.当滑块放到皮带上时,弹簧的轴线恰好水平,若滑块放到皮带上的瞬间,滑块的速度为零,且弹簧正好处于自由长度,则当弹簧第一次伸长到最大时,滑块与皮带间所产生的热量是多少?(已知弹簧振子周期T=2π| m/k |
(8分) 一皮带传动装置如图所示,皮带的速度v足够大.一根质量不计、劲度系数为k的弹簧一端固定,另一端连接一个质量为m的滑块,已知滑块与皮带间的动摩擦因数为μ.当滑块放到皮带上时,弹簧的轴线恰好水平,若滑块放到皮带上的瞬间,滑块的速度为零,且弹簧正好处于自由长度,则当弹簧第一次伸长到最大时,滑块与皮带间所产生的热量是多少?(已知弹簧振子周期![]() )
)
A.t1=t2 B.t1<t2
C.t1>t2 D.无法判断
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com