
题目列表(包括答案和解析)
| 1 |
| g |
| 4π2 |
| g |
| g |
| 4π2 |
| 4π2△l | ||||
|
| 4π2△l | ||||
|
| t |
| n |
| t |
| n |
| gT2 |
| 4π2 |
 (1)有以下说法:
(1)有以下说法:| t | n |
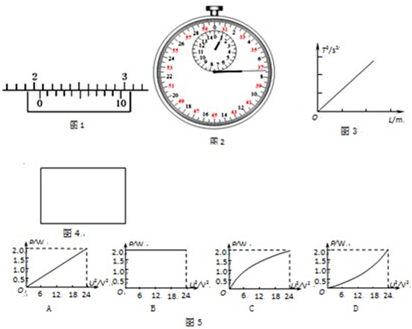
某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆摆动过程中的摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t;在测量单摆的摆长时,先用毫米刻度尺测得悬挂后的摆线长(从悬点到摆球的最上端)为L,再用游标卡尺测得摆球的直径为d.
(1)用上述物理量的符号写出求重力加速度的一般表达式g = .
(2)实验结束后,某同学发现他测得的重力加速度的值总是偏大,其原因可能是下述原因中的 .
A.单摆的悬点未固定紧,振动中出现松动,使摆线增长了
B.把n次摆动的时间误记为(n + 1)次摆动的时间
C.以摆线长作为摆长来计算
D.以摆线长与摆球的直径之和作为摆长来计算
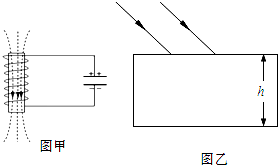
(3) 某同学在做“用单摆测定重力加速度”的实验中,用秒表测单摆完成40次全振动的时间如图所示,则单摆的周期为______________s。
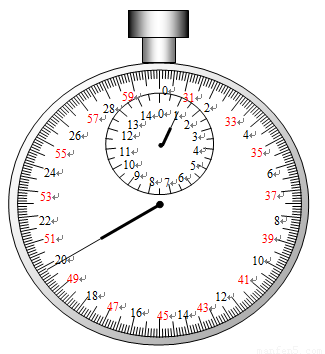
(4)为了提高实验精度,在实验中可改变几次摆长L并测出相应的周期T,从而得出一组对应的L与T的数据,再以L为横坐标、T2为纵坐标将所得数据连成直线,并求得该直线的斜率k。则重力加速度g=________ 。(用k表示)若根据所得数据连成的直线的延长线没过坐标原点,而是与纵轴的正半轴相交于一点,则实验过程中可能存在的失误是 ,因此失误,由图象求得的重力加速度的g (偏大,偏小,无影响)
某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆摆动过程中的摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t;在测量单摆的摆长时,先用毫米刻度尺测得悬挂后的摆线长(从悬点到摆球的最上端)为L,再用游标卡尺测得摆球的直径为d.
(1)用上述物理量的符号写出求重力加速度的一般表达式g = .
(2)实验结束后,某同学发现他测得的重力加速度的值总是偏大,其原因可能是下述原因中的 .
A.单摆的悬点未固定紧,振动中出现松动,使摆线增长了
B.把n次摆动的时间误记为(n + 1)次摆动的时间
C.以摆线长作为摆长来计算
D.以摆线长与摆球的直径之和作为摆长来计算
(3) 某同学在做“用单摆测定重力加速度”的实验中,用秒表测单摆完成40次全振动的时间如图所示,则单摆的周期为______________s。
(4)为了提高实验精度,在实验中可改变几次摆长L并测出相应的周期T,从而得出一组对应的L与T的数据,再以L为横坐标、T2为纵坐标将所得数据连成直线,并求得该直线的斜率k。则重力加速度g=________ 。(用k表示)若根据所得数据连成的直线的延长线没过坐标原点,而是与纵轴的正半轴相交于一点,则实验过程中可能存在的失误是 ,因此失误,由图象求得的重力加速度的g (偏大,偏小,无影响)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com