
题目列表(包括答案和解析)
(本小题满分5分)已知菱形纸片ABCD的边长为![]() ,∠A=60°,E为
,∠A=60°,E为![]() 边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点
边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点![]() 处,过点
处,过点![]() 作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点
作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点![]() 处,
处,![]() 与
与![]() H分别交
H分别交![]() 与
与![]() 于点M、N.若点
于点M、N.若点![]() 在△
在△![]() EF的内部或边上,此时我们称四边形
EF的内部或边上,此时我们称四边形![]() (即图中阴影部分)为“重叠四边形”.
(即图中阴影部分)为“重叠四边形”.
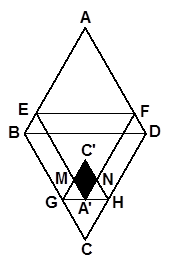


图1 图2 备用图
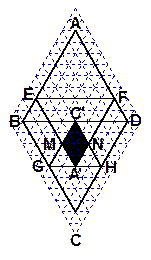
(1)若把菱形纸片ABCD放在菱形网格中(图中每个小三角形都是边长为1的等边三角形),点A、B、C、D、E恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠四边形![]() 的面积;
的面积;
(2)实验探究:设AE的长为![]() ,若重叠四边形
,若重叠四边形![]() 存在.试用含
存在.试用含![]() 的代数式表示重叠四边形
的代数式表示重叠四边形![]() 的面积,并写出
的面积,并写出![]() 的取值范围(直接写出结果,备用图供实验,探究使用).
的取值范围(直接写出结果,备用图供实验,探究使用).
 ,∠A=60°,E为
,∠A=60°,E为 边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点
边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点 处,过点
处,过点 作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点
作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点 处,
处, 与
与 H分别交
H分别交 与
与 于点M、N.若点
于点M、N.若点 在△
在△ EF的内部或边上,此时我们称四边形
EF的内部或边上,此时我们称四边形 (即图中阴影部分)为“重叠四边形”.
(即图中阴影部分)为“重叠四边形”.


 | |||
 | |||
 的面积;
的面积; ,若重叠四边形
,若重叠四边形 存在.试用含
存在.试用含 的代数式表示重叠四边形
的代数式表示重叠四边形 的面积,并写出
的面积,并写出 的取值范围(直接写出结果,备用图供实验,探究使用).
的取值范围(直接写出结果,备用图供实验,探究使用).(本小题满分5分)已知菱形纸片ABCD的边长为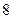 ,∠A=60°,E为
,∠A=60°,E为 边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点
边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点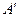 处,过点
处,过点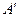 作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点
作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点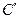 处,
处,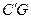 与
与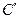 H分别交
H分别交 与
与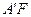 于点M、N.若点
于点M、N.若点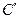 在△
在△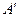 EF的内部或边上,此时我们称四边形
EF的内部或边上,此时我们称四边形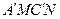 (即图中阴影部分)为“重叠四边形”.
(即图中阴影部分)为“重叠四边形”.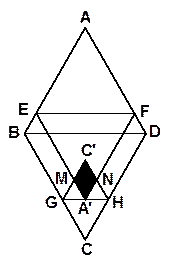

 | |||
 | |||
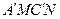 的面积;
的面积;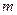 ,若重叠四边形
,若重叠四边形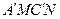 存在.试用含
存在.试用含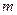 的代数式表示重叠四边形
的代数式表示重叠四边形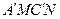 的面积,并写出
的面积,并写出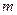 的取值范围(直接写出结果,备用图供实验,探究使用).
的取值范围(直接写出结果,备用图供实验,探究使用).(本小题满分5分)已知菱形纸片ABCD的边长为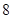 ,∠A=60°,E为
,∠A=60°,E为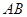 边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点
边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点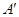 处,过点
处,过点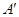 作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点
作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点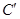 处,
处,
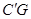 与
与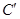 H分别交
H分别交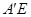 与
与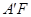 于点M、N.若点
于点M、N.若点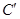 在△
在△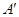 EF的内部或边上,此时我们称四边形
EF的内部或边上,此时我们称四边形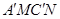 (即图中阴影部分)为“重叠四边形”.
(即图中阴影部分)为“重叠四边形”.
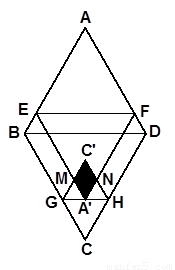
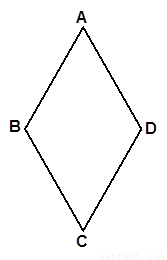

 |
|||
 |
图1 图2 备用图
(1)若把菱形纸片ABCD放在菱形网格中(图中每个小三角形都是边长为1的等边三角形),点A、B、C、D、E恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠四边形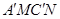 的面积;
的面积;
(2)实验探究:设AE的长为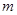 ,若重叠四边形
,若重叠四边形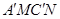 存在.试用含
存在.试用含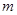 的代数式表示重叠四边形
的代数式表示重叠四边形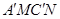 的面积,并写出
的面积,并写出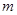 的取值范围(直接写出结果,备用图供实验,探究使用).
的取值范围(直接写出结果,备用图供实验,探究使用).
 ,∠A=60°,E为
,∠A=60°,E为 边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点
边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点 处,过点
处,过点 作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点
作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点 处,
处,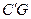 与
与 H分别交
H分别交 与
与 于点M、N.若点
于点M、N.若点 在△
在△ EF的内部或边上,此时我们称四边形
EF的内部或边上,此时我们称四边形 (即图中阴影部分)为“重叠四边形”.
(即图中阴影部分)为“重叠四边形”.


 | |||
 | |||
 的面积;
的面积; ,若重叠四边形
,若重叠四边形 存在.试用含
存在.试用含 的代数式表示重叠四边形
的代数式表示重叠四边形 的面积,并写出
的面积,并写出 的取值范围(直接写出结果,备用图供实验,探究使用).
的取值范围(直接写出结果,备用图供实验,探究使用).湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com