
题目列表(包括答案和解析)
 (1)求右焦点坐标是(2,0),且经过点(-2,-
(1)求右焦点坐标是(2,0),且经过点(-2,-| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
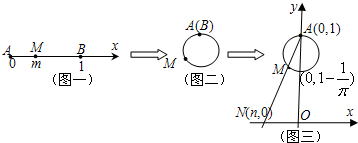 如图揭示了一个由区间(0,1)到实数集R上的对应过程:区间(0,1)内的任意实数m与数轴上的线段AB(不包括端点)上的点M一一对应(图一),将线段AB围成一个圆,使两端A,B恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1)(图三).图三中直线AM与x轴交于点N(n,0),由此得到一个函数n=f(m),则下列命题中正确的序号是( )
如图揭示了一个由区间(0,1)到实数集R上的对应过程:区间(0,1)内的任意实数m与数轴上的线段AB(不包括端点)上的点M一一对应(图一),将线段AB围成一个圆,使两端A,B恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1)(图三).图三中直线AM与x轴交于点N(n,0),由此得到一个函数n=f(m),则下列命题中正确的序号是( )| 1 |
| 2 |
| 1 |
| 2 |
| A、(1)(3)(4) |
| B、(1)(2)(3) |
| C、(1)(2)(4) |
| D、(1)(2)(3)(4) |
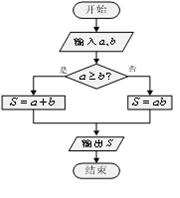
 (2012•泉州模拟)定义一种运算S=a?b,在框图所表达的算法中揭示了这种运算“?”的含义.那么,按照运算“?”的含义,计算tan15°?tan30°+tan30°?tan15°=
(2012•泉州模拟)定义一种运算S=a?b,在框图所表达的算法中揭示了这种运算“?”的含义.那么,按照运算“?”的含义,计算tan15°?tan30°+tan30°?tan15°= (I)已知椭圆C的方程是
(I)已知椭圆C的方程是| x2 |
| a2 |
| y2 |
| b2 |
定义一种运算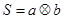 ,在框图所表达的算法中揭示了这种运算“
,在框图所表达的算法中揭示了这种运算“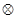 ”的含义.那么,按照运算“
”的含义.那么,按照运算“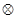 ”的含义,计算
”的含义,计算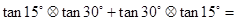 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com