
题目列表(包括答案和解析)
(09年湖南师大附中月考理)(13分)
某加工厂需定期购买原材料,已知每公斤原材料的价格为1.5元,每次购买原材料需支付运费600元,每公斤原材料每天的保管费用为0.03元,该厂每天需要消耗原材料400公斤,每次购买的原材料当天即开始使用(即有400公斤不需要保管)。
(1)设该厂每![]() 天购买一次原材料,试写出每次购买的原材料在
天购买一次原材料,试写出每次购买的原材料在![]() 天内总的保管费用
天内总的保管费用![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(本小题满分13分)
某电视生产企业有A、B两种型号的电视机参加家电下乡活动,若企业投放A、B两种型号电视机的价值分别为a、b万元,则农民购买电视机获得的补贴分别为 万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
(1)请你选择自变量,将这次活动中农民得到的总补贴表示为它的函数,并求其定义域;
(2)求当投放B型电视机的金额为多少万元时,农民得到的总补贴最大?
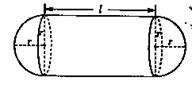
(本小题满分13分).某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为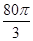 立方米,且
立方米,且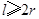 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为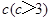 千元,设该容器的建造费用为
千元,设该容器的建造费用为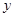 千元.
千元.
(Ⅰ)写出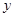 关于
关于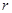 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的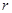 .
.
(本小题满分13分)
某学生在上学路上要经过4个路口,假设在 各路口是否遇到红灯是相互独立的,遇到红灯的概率都是
各路口是否遇到红灯是相互独立的,遇到红灯的概率都是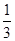 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min.
(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(Ⅱ)求这名学生在上学路上因遇到红灯停留的总时间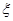 的分布列及期望.
的分布列及期望.
(本小题满分13分)
某建筑工地在一块长AM=30米,宽AN=20米的矩形地块AMPN上施工,规划建设占地如图中矩形ABCD的学生公寓,要求顶点C在地块的对角线MN上,B,D分别在边AM,AN上,假设AB长度为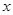 米。
米。
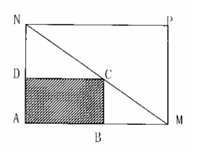
(1)要使矩形学生公寓ABCD的面积不小于144平方米,AB的长度应在什么范围?
(2)长度AB和宽度AD分别为多少米时矩形学生公寓ABCD的面积最大?最大值是多少平方米?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com