
题目列表(包括答案和解析)
在数列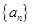 中,
中,
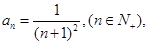 记
记
(Ⅰ)求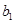 、
、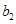 、
、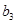 、
、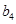 并推测
并推测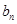 ;
;
(Ⅱ)用数学归纳法证明你的结论.
【解析】第一问利用递推关系可知,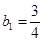 、
、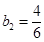 、
、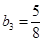 、
、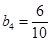 ,猜想可得
,猜想可得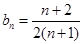
第二问中,①当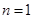 时,
时,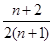 =
=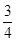 ,又
,又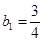 ,猜想正确
,猜想正确
②假设当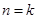 时猜想成立,即
时猜想成立,即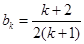 ,
,
当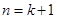 时,
时,
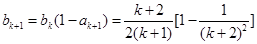 =
=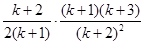
=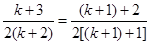 ,即当
,即当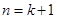 时猜想也成立
时猜想也成立
两步骤得到。
(2)①当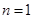 时,
时,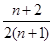 =
=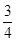 ,又
,又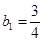 ,猜想正确
,猜想正确
②假设当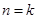 时猜想成立,即
时猜想成立,即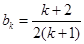 ,
,
当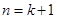 时,
时,
 =
=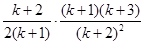
=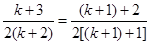 ,即当
,即当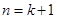 时猜想也成立
时猜想也成立
由①②可知,对于任何正整数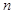 都有
都有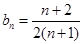 成立
成立
⊙O1和⊙O2的极坐标方程分别为 ,
, .
.
⑴把⊙O1和⊙O2的极坐标方程化为直角坐标方程;
⑵求经过⊙O1,⊙O2交点的直线的直角坐标方程.
【解析】本试题主要是考查了极坐标的返程和直角坐标方程的转化和简单的圆冤啊位置关系的运用
(1)中,借助于公式 ,
, ,将极坐标方程化为普通方程即可。
,将极坐标方程化为普通方程即可。
(2)中,根据上一问中的圆的方程,然后作差得到交线所在的直线的普通方程。
解:以极点为原点,极轴为x轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
(I) ,
, ,由
,由 得
得 .所以
.所以 .
.
即 为⊙O1的直角坐标方程.
为⊙O1的直角坐标方程.
同理 为⊙O2的直角坐标方程.
为⊙O2的直角坐标方程.
(II)解法一:由 解得
解得 ,
,
即⊙O1,⊙O2交于点(0,0)和(2,-2).过交点的直线的直角坐标方程为y=-x.
解法二: 由 ,两式相减得-4x-4y=0,即过交点的直线的直角坐标方程为y=-x
,两式相减得-4x-4y=0,即过交点的直线的直角坐标方程为y=-x
已知函数 .]
.]
(1)求函数 的最小值和最小正周期;
的最小值和最小正周期;
(2)设 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 ,
, ,
, ,且
,且 ,
, ,
,
若 ,求
,求 ,
, 的值.
的值.
【解析】第一问利用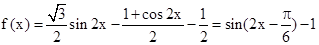
得打周期和最值
第二问

 ,由正弦定理,得
,由正弦定理,得 ,①
,①
由余弦定理,得 ,即
,即 ,②
,②
由①②解得
 由计算机随机选出大批正整数,取其最高位数字(如 35为3,110为1)的次数构成一个分布,已知这个分布中,数字1,2,3,…,9出现的概率正好构成一个首项为
由计算机随机选出大批正整数,取其最高位数字(如 35为3,110为1)的次数构成一个分布,已知这个分布中,数字1,2,3,…,9出现的概率正好构成一个首项为| 1 | 5 |
| x2 |
| 2 |
| x3 |
| 3 |
| xn |
| n |
一、选择题
1. D
解析:∵a3+a7+a11=3a7为常数,
∴S13= =13a7,也是常数.
=13a7,也是常数.
2. C
解析:∵易知q≠1,S6∶S3=1∶2
 =
= ,q3=-
,q3=- ,
,
∴S9∶S3= =1+q3+q6=1-
=1+q3+q6=1- +(-
+(- )2=
)2= .
.
3.A  ,
,
又


4.D 数列 是以2为首项,以
是以2为首项,以 为公比的等比数列,项数为
为公比的等比数列,项数为 故选D。
故选D。
5.B
6. D
解析:当q=1时,Sn,Sn+1,Sn+2构成等差数列;
当q=-2时,Sn+1,Sn,Sn+2构成等差数列;
当q=- 时,Sn,Sn+2,Sn+1构成等差数列.
时,Sn,Sn+2,Sn+1构成等差数列.
7.A 仅②不需要分情况讨论,即不需要用条件语句
8. D
9. D
解析:易知an=
∴a13+a23+…+an3=23+81+82+…+8n-1=8+ =
= (8n-1+6).
(8n-1+6).
10.A提示:依题意 可得.
可得.
11.B, 指输入的数据.
指输入的数据.
12.D
(法一)辗转相除法:


∴ 是
是 和
和 的最大公约数.
的最大公约数.
(法二)更相减损术:





 ∴
∴ 是
是 和
和 的最大公约数.
的最大公约数.
二、填空题
13.

14. 

当 时,
时, 是正整数。
是正整数。
15.
解析:bn= =
= =a1
=a1 ,bn+1=a1
,bn+1=a1 ,
, =
= (常数).
(常数).
16.-6
三、解答题
17.解(1)

 以3为公比的等比数列.
以3为公比的等比数列.
(2)由(1)知, .
. .
.
 不适合上式,
不适合上式,
 .
.
18.解:(1)an=
 (2)
(2) .
.
19.解:(1) ,
, ;
;
(2)由(1)得 ,假设数列{bn}中存在三项bp,bq,br(p,q,r互不相等)成等比数列,则
,假设数列{bn}中存在三项bp,bq,br(p,q,r互不相等)成等比数列,则 即
即
∴ ,
, ,
, ,得
,得
∴p=r,矛盾. ∴数列{bn}中任意三项都不可能成等比数列.
20.解:设未赠礼品时的销售量为a0个,而赠送礼品价值n元时销售量为an个,
 ,
,
又设销售利润为数列 ,
,
当 ,
,
考察 的单调性,
的单调性,

 当n=9或10时,
当n=9或10时, 最大
最大
答:礼品价值为9元或10元时商品获得最大利润.
21.解析:(1) 时,
时,
 即
即
两式相减:
即 故有
故有
 。
。
 数列
数列 为首项
为首项 公比
公比 的等比数列。
的等比数列。

(2)
 则
则

又
(3)
 ①
①
而 ②
②
①-②得:

22.解:(1)b4=b1+3d 即11=2+3d, ∴b1=2,
b2=5, b3=8, b4=11,
b5=8, b6=5, b7=2;
∴b1=2,
b2=5, b3=8, b4=11,
b5=8, b6=5, b7=2;
(2)S=C1+C2+…+C49=2(C25+C26+…+C49)-C25= ;
;
(3) ,d100=2+3×49=149,∴d1, d2,…d50是首项为149,公差为-3的等差数列.
,d100=2+3×49=149,∴d1, d2,…d50是首项为149,公差为-3的等差数列.
当n≤50时,
当51≤n≤100时,Sn=d1+d2+…d50=S50+(d51+d52+…dn)
=3775+(n-50)×2+ =
=
∴综上所述, .
.
w.w.w.k.s.5.u.c.o.m

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com