练习册

  • 练习册
  • 试题
    等比数列的常用性质:已知是等比数列.公比为.则 【查看更多】

     

    题目列表(包括答案和解析)

    定义：若一个数列中的每一项都是另一个数列中的项，则称这个数列是另一个数列的子数列。已知是等差数列，是公比为的等比数列，，，记为数列的前项和．

    （Ⅰ）若（是大于的正整数），求证：；

    （Ⅱ）若（是某个正整数），求证：是整数，且数列是数列的子数列.

    查看答案和解析>>

    定义：若一个数列中的每一项都是另一个数列中的项，则称这个数列是另一个数列的子数列。已知是等差数列，是公比为的等比数列，，，记为数列的前项和．

    （Ⅰ）若（是大于的正整数），求证：；

    （Ⅱ）若（是某个正整数），求证：是整数，且数列是数列的子数列.

    查看答案和解析>>

    （本题满分12分）

    定义：若一个数列中的每一项都是另一个数列中的项，则称这个数列是另一个数列的子数列。已知是等差数列，是公比为的等比数列，，，记为数列的前项和．

    （Ⅰ）若（是大于的正整数），求证：；

    （Ⅱ）若（是某个正整数），求证：是整数，且数列是数列的子数列.

    查看答案和解析>>

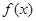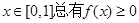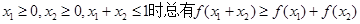    （12分）对定义在[0, 1]上并且满足下列两个条件的函数称为G函数。①对任意的，②成立。已知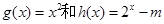是定义在[0, 1]上的函数。

    （1）问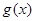是否为G函数，说明理由；

    （2）若是G函数，求实数m取值的范围。

     

    查看答案和解析>>

    设函数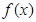的定义域为R，如果存在函数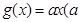为常数），使得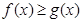对于一切实数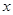都成立，那么称为函数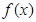的一个承托函数. 已知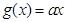是函数的一个承托函数，那么实数a的取值范围是（    ）

    A.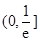

    B.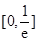

    C.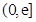  

    D.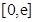

     

    查看答案和解析>>

     

    一、选择题

    1. D

    解析:∵a3+a7+a11=3a7为常数，

    ∴S13==13a7，也是常数.

    2. C

    解析:∵易知q≠1,S6∶S3=1∶2=,q3=-,

    ∴S9∶S3==1+q3+q6=1-+(-)2=.

    3．A ，

    又

    4．D  数列是以2为首项，以为公比的等比数列，项数为故选D。

    5.B

    6. D

    解析:当q=1时，Sn,Sn+1,Sn+2构成等差数列；

    当q=-2时，Sn+1,Sn,Sn+2构成等差数列；

    当q=-时，Sn,Sn+2,Sn+1构成等差数列.

    ７．A   仅②不需要分情况讨论，即不需要用条件语句

     

    8. D

    9. D

    解析:易知an=

    ∴a13+a23+…+an3=23+81+82+…+8n-1=8+=(8n-1+6).

    10.A提示：依题意可得.

    １１．B，指输入的数据．

    １２．D 

    （法一）辗转相除法：         

    ∴是和的最大公约数．

    （法二）更相减损术：

            

            ∴是和的最大公约数．

    二、填空题

    13.

    14.

    当时，是正整数。

    15.

    解析:bn===a1,bn+1=a1,=(常数).

    16．-6

    三、解答题

    17．解（1）

         

          以3为公比的等比数列.

     （2）由（1）知，..

          不适合上式，

           .

    18．解：（1）an=    （2）.

    19．解：(1)，；

    （2）由（1）得，假设数列{bn}中存在三项bp,bq,br(p,q,r互不相等)成等比数列，则 即

    ∴，，，得

    ∴p=r，矛盾.  ∴数列{bn}中任意三项都不可能成等比数列.

    20.解：设未赠礼品时的销售量为a0个，而赠送礼品价值n元时销售量为an个，

    ，

    又设销售利润为数列，

    当，

    考察的单调性，

    当n=9或10时，最大

    答：礼品价值为9元或10元时商品获得最大利润.

     

    21.解析：（1）时，

    即

    两式相减：

    即故有

    。

    数列为首项公比的等比数列。

    （2）

    则

    又

    （3）

       ①

    而   ②

    ①-②得：

    22.解：（1）b4=b1＋3d  即11=2＋3d， ∴b1=2, b2=5, b3=8, b4=11, b5=8, b6=5, b7=2；

    （2）S=C1＋C2＋…＋C49=2(C25＋C26＋…＋C49)－C25=；

    （3）,d100=2＋3×49=149，∴d1, d2,…d50是首项为149，公差为－3的等差数列.  

    当n≤50时，

    当51≤n≤100时,Sn=d1＋d2＋…d50=S50＋(d51＋d52＋…dn)

                       =3775＋(n－50)×2＋=

    ∴综上所述,.

    w.w.w.k.s.5.u.c.o.m

     

     


    同步练习册答案