
题目列表(包括答案和解析)
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、a<b<c |
| B、b<c<a |
| C、b<a<c |
| D、c<a<b |
|
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 3 |
| A、①③ | B、②④ |
| C、①③④ | D、①②③④ |
|
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 3 |
| 1 |
| 4 |
已知函数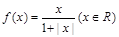 时,则下列结论不正确的是
.
时,则下列结论不正确的是
.
(1)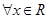 ,等式
,等式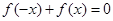 恒成立
恒成立
(2)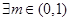 ,使得方程
,使得方程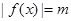 有两个不等实数根
有两个不等实数根
(3)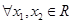 ,若
,若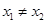 ,则一定有
,则一定有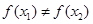
(4)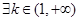 ,使得函数
,使得函数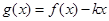 在
在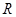 上有三个零点
上有三个零点
已知函数 ,现给出下列命题:
,现给出下列命题:
① 当图象是一条连续不断的曲线时,则 =
=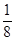 ;
;
② 当图象是一条连续不断的曲线时,能找到一个非零实数 ,使得f (x)在R上是增函数;
,使得f (x)在R上是增函数;
③ 当 时,不等式
时,不等式 恒成立;
恒成立;
④ 函数 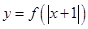 是偶函数 . 其中正确的命题是 ( )
是偶函数 . 其中正确的命题是 ( )
A . ①③ B. ②④ C. ①③④ D . ①②③④
.files\image019.jpg)
.files\image019.jpg) 一、选择题:本大题共12小题,每小题5分,共60分。
一、选择题:本大题共12小题,每小题5分,共60分。
.files\image019.jpg) 1―5 DABBA 6―10 DDCCB 11―12 AC
1―5 DABBA 6―10 DDCCB 11―12 AC
.files\image019.jpg) 二、填空题:本大题共4小题,每小题5分,共20分。
二、填空题:本大题共4小题,每小题5分,共20分。
.files\image019.jpg) 13.
13..files\image149.gif) 14.
14..files\image151.gif) 15.
15..files\image153.gif) 16.②④
16.②④
.files\image019.jpg) 三、解答题:本大题共6小题,满分70分。
三、解答题:本大题共6小题,满分70分。
.files\image019.jpg) 17.(本小题满分10分)
17.(本小题满分10分)
.files\image019.jpg) (I)解:
(I)解:
.files\image019.jpg)
.files\image155.gif) 时,
时,
.files\image019.jpg)
.files\image157.gif) ………………2分
………………2分
.files\image019.jpg)
.files\image159.gif) ………………4分
………………4分
.files\image019.jpg)
.files\image161.gif) ,
,
.files\image019.jpg)
.files\image163.gif) ………………5分
………………5分
.files\image019.jpg) (II)解:
(II)解:
.files\image019.jpg)
.files\image165.gif)
.files\image019.jpg) 18.(本小题满分12分)
18.(本小题满分12分)
.files\image019.jpg) (I)解:
(I)解:
.files\image019.jpg)
.files\image167.gif)
.files\image019.jpg)
.files\image169.gif)
.files\image019.jpg) (II)解:
(II)解:
.files\image019.jpg) 由(I)知:
由(I)知:.files\image171.gif)
.files\image019.jpg)
.files\image173.gif)
.files\image019.jpg) (III)解:
(III)解:
.files\image019.jpg)
|