
题目列表(包括答案和解析)
(本小题满分13分) 已知双曲线![]() 的两个焦点为
的两个焦点为![]() 的曲线C上.
的曲线C上.
(Ⅰ)求双曲线C的方程;
(Ⅱ)记O为坐标原点,过点Q (0,2)的直线l与双曲线C相交于不同的两点E、F,若△OEF的面积为![]() 求直线l的方程
求直线l的方程
(本小题满分13分)
已知双曲线 的右顶点为A,右焦点为F,右准线与
的右顶点为A,右焦点为F,右准线与 轴交于点B,且与一条渐近线交于点C,点O为坐标原点,又
轴交于点B,且与一条渐近线交于点C,点O为坐标原点,又 ,
, 过点F的直线与双曲线右交于点M、N,点P为点M关于
过点F的直线与双曲线右交于点M、N,点P为点M关于 轴的对称点。
轴的对称点。
(1)求双曲线的方程;
(2)证明:B、P、N三点共线;
(3)求 面积的最小值。
面积的最小值。
(本小题满分13分)已知双曲线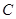 的焦点为
的焦点为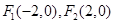 ,且离心率为2;
,且离心率为2;
(Ⅰ)求双曲线的标准方程;
(Ⅱ)若经过点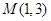 的直线
的直线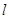 交双曲线
交双曲线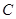 于
于 两点,且
两点,且 为
为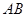 的中点,求直线
的中点,求直线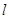 的方程。
的方程。
(本小题满分13分)
已知双曲线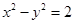 的右焦点为
的右焦点为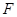 ,过点
,过点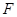 的动直线与双曲线相交于
的动直线与双曲线相交于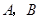 两点,点
两点,点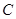 的坐标是
的坐标是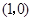 .
.
(I)证明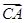 ,
,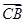 为常数;
为常数;
(II)若动点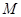 满足
满足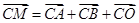 (其中
(其中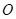 为坐标原点),求点
为坐标原点),求点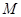 的轨迹方程.
的轨迹方程.
(本小题满分13分)
已知双曲线 的两条渐近线分别为
的两条渐近线分别为 .
.
(1)求双曲线 的离心率;
的离心率;
(2)如图, 为坐标原点,动直线
为坐标原点,动直线 分别交直线
分别交直线 于
于 两点(
两点( 分别在第一,四象限),且
分别在第一,四象限),且 的面积恒为8,试探究:是否存在总与直线
的面积恒为8,试探究:是否存在总与直线 有且只有一个公共点的双曲线
有且只有一个公共点的双曲线 ?若存在,求出双曲线
?若存在,求出双曲线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
高考资源网版权所有
一、DBCCC DCADB
二、11.72 12..files\image129.gif) 13.
13..files\image131.gif) 14.
14..files\image133.gif) 15.
15..files\image135.gif)
三、16.(Ⅰ).files\image137.gif) .
.
∵.files\image139.gif) ,∴
,∴.files\image141.gif) ,∴
,∴.files\image143.gif) ,∴当
,∴当.files\image145.gif) 时,f(A)取最小值
时,f(A)取最小值.files\image147.gif) .
.
(Ⅱ)由(Ⅰ)知, .files\image149.gif) 时,
时, .files\image145.gif) .于是
.于是.files\image151.gif) ,
,
由.files\image153.gif) 得
得.files\image155.gif) .
.
17.(Ⅰ)设“从甲盒内取出的2个球均为黑球”为事件.files\image157.gif) ,“从乙盒内取出的2个球均为黑球”为事件
,“从乙盒内取出的2个球均为黑球”为事件.files\image159.gif) .由于事件
.由于事件.files\image161.gif) 相互独立,且
相互独立,且.files\image163.gif) ,
,.files\image165.gif) .
.
故取出的4个球均为黑球的概率为.files\image167.gif) .
.
(Ⅱ)设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件.files\image169.gif) ,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件
,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件.files\image171.gif) .由于事件
.由于事件.files\image173.gif) 互斥,
互斥,
且.files\image175.gif) ,
,.files\image177.gif) .
.
故取出的4个球中恰有1个红球的概率为.files\image179.gif) .
.
(Ⅲ)取出的4个球中红球的个数为0,1,2,3时的概率分别记为.files\image181.gif) .由(Ⅰ),(Ⅱ)得
.由(Ⅰ),(Ⅱ)得.files\image183.gif) ,
,.files\image185.gif) ,
,.files\image187.gif) .从而
.从而.files\image189.gif) .
.
18.(I)∵AB∥CD,AD=DC=CB=a,∴四边形ABCD是等腰梯形.设AC交BD于N,连EN.
∵∠ABC=60°,∴∠DCB=∠ADC=120°,∠DAC=∠ACD=30°,
.files\image190.jpg) ∴AC=
∴AC=.files\image192.gif) ,AB=2a,
,AB=2a,.files\image194.gif) =90°.
=90°.
又四边形ACEF是矩形,
∴AC⊥平面BCE.∴AC⊥BE.
(II)∵平面ACEF⊥平面ABCD, EC⊥AC,
∴EC⊥面 ABCD,∴EC⊥CD, EC⊥AD,又AF∥CE,
∴AF⊥AD,而AF=CE,AD=CD,
∴Rt△.files\image196.gif) ≌Rt△
≌Rt△.files\image198.gif) ,DE=DF.
,DE=DF.
过D作DG⊥EF于G,则G为EF的中点,于是EG=.files\image200.gif) .
.
在Rt△.files\image202.gif) 中,
中,.files\image204.gif)
.files\image206.gif) ,∴
,∴.files\image208.gif) .∴
.∴.files\image210.gif) .
.
设所求二面角大小为.files\image212.gif) ,则由
,则由.files\image214.gif) 及
及.files\image216.gif) ,
,.files\image218.gif) 得,
得,.files\image220.gif) ,
,
www.ks5u.com
.files\image222.jpg) .21.(I)由于椭圆过定点A(1,0),于是a=1,c=
.21.(I)由于椭圆过定点A(1,0),于是a=1,c=.files\image224.gif) .
.
∵ .files\image226.gif) ,∴
,∴.files\image228.gif) .
.
(Ⅱ)解方程组.files\image230.gif) ,得
,得.files\image232.gif) .
.
∵.files\image234.gif) ,∴
,∴.files\image236.gif) .
.
(Ⅲ)设抛物线方程为:.files\image238.gif) .
.
又∵.files\image240.gif) ,∴
,∴.files\image242.gif) .
.
又.files\image244.gif) ,得
,得.files\image246.gif) .
.
令.files\image248.gif) .
.
∵.files\image250.gif) 内有根且单调递增,
内有根且单调递增,
∴.files\image252.gif)
∴.files\image254.gif)
故.files\image256.gif) .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com