
题目列表(包括答案和解析)
在数列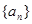 中,
中,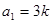 ,其中
,其中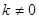 ,对任意
,对任意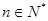 都有:
都有: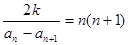 ;(1)求数列
;(1)求数列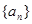 的第2项和第3项;
的第2项和第3项;
(2)求数列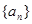 的通项公式
的通项公式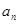 ,假设
,假设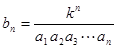 ,试求数列
,试求数列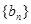 的前
的前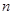 项和
项和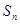 ;
;
(3)若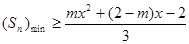 对一切
对一切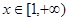 恒成立,求
恒成立,求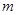 的取值范围。
的取值范围。
【解析】第一问中利用)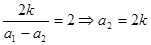 同理得到
同理得到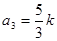
第二问中,由题意得到: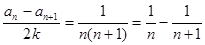
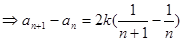
累加法得到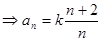
第三问中,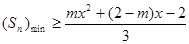 利用恒成立,转化为最小值大于等于即可。得到范围。
利用恒成立,转化为最小值大于等于即可。得到范围。
(1)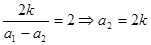 同理得到
同理得到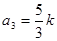 ……2分
……2分
(2)由题意得到: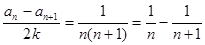
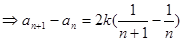
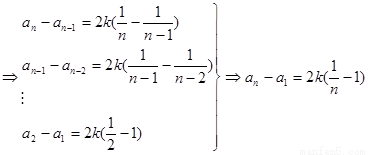 又
又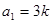
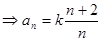 ……5分
……5分
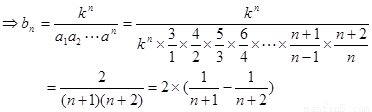
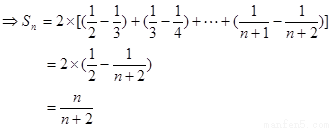 ……8分
……8分
(3)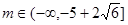
课外研究题:将一块圆心角为![]() ,半径为20厘米的扇形铁片裁成一块矩形,请你设计裁法,使裁得矩形的面积最大?并说明理由.
,半径为20厘米的扇形铁片裁成一块矩形,请你设计裁法,使裁得矩形的面积最大?并说明理由.
教学建议:这是一个研究性学习内容,可让学生在课外两人一组合作完成,写成研究报告,在习题课上让学生交流研究结果,老师可适当进行点评。
参考答案:这是一个如何下料的问题,一般有如图(1)、图(2)的两种裁法:即让矩形一边在扇形的一条半径![]() 上,或让矩形一边与弦
上,或让矩形一边与弦![]() 平行。从图形的特点来看,涉及到线段的长度和角度,将这些量放置在三角形中,通过解三角形求出矩形的边长,再计算出两种方案所得矩形的最大面积,加以比较,
平行。从图形的特点来看,涉及到线段的长度和角度,将这些量放置在三角形中,通过解三角形求出矩形的边长,再计算出两种方案所得矩形的最大面积,加以比较,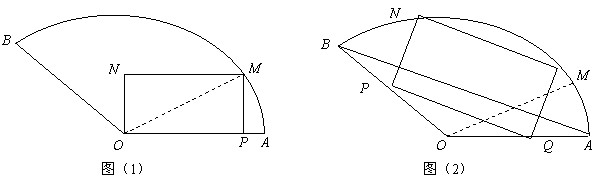 就可以得出问题的结论.
就可以得出问题的结论.
已知数列 中,
中, ,
, ,数列
,数列 中,
中, ,且点
,且点 在直线
在直线 上。
上。
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 ;
;
(3)若 ,求数列
,求数列 的前
的前 项和
项和 ;
;
【解析】第一问中利用数列的递推关系式
 ,因此得到数列
,因此得到数列 的通项公式;
的通项公式;
第二问中, 在
在 即为:
即为:
即数列 是以
是以 的等差数列
的等差数列
得到其前n项和。
第三问中, 又
又 

 ,利用错位相减法得到。
,利用错位相减法得到。
解:(1)
 即数列
即数列 是以
是以 为首项,2为公比的等比数列
为首项,2为公比的等比数列

 ……4分
……4分
(2) 在
在 即为:
即为:
即数列 是以
是以 的等差数列
的等差数列

 ……8分
……8分
(3) 又
又 


 ①
①  ②
②
①- ②得到




为了让学生更多的了解“数学史”知识,某中学高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,统计结果见下表.请你根据频率分布表解答下列问题:
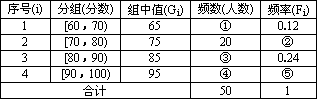
(1)填充频率分布表中的空格.(把结果填在相应的横线上即可)
(2)在上述统计数据的分析中有一项计算见算法流程图,求输出的S的值.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com