
题目列表(包括答案和解析)
(本小题满分14分)集合A是由适合以下性质的函数![]() 构成的;对于任意的
构成的;对于任意的![]() ,都有
,都有![]()
(1)分别判断函数![]() 是否在集合A中?并说明理由;
是否在集合A中?并说明理由;
(2)设函数![]() ,试求|2a+b|的取值范围;
,试求|2a+b|的取值范围;
(3)在(2)的条件下,若![]() ,且对于满足(2)的每个实数a,存在最小的实数m,使得当
,且对于满足(2)的每个实数a,存在最小的实数m,使得当![]() 恒成立,试求用a表示m的表达式.
恒成立,试求用a表示m的表达式.
(本小题满分13分)
设M是由满足下列条件的函数 构成的集合:“①方程
构成的集合:“①方程 有实数根;②函数
有实数根;②函数 的导数
的导数 满足
满足 ”.
”.
(1)判断函数 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(2)若集合M中的元素具有下面的性质:“若 的定义域为D,则对于任意
的定义域为D,则对于任意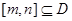 ,都存在
,都存在 ,使得等式
,使得等式 成立”,试用这一性质证明:方程
成立”,试用这一性质证明:方程 只有一个实数根;
只有一个实数根;
(3)设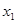 是方程
是方程 的实数根,求证:对于
的实数根,求证:对于 定义域中的任意的
定义域中的任意的 ,当
,当 且
且 时,
时,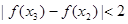 .
.
(本小题满分13分)
设M是由满足下列条件的函数 构成的集合:“①方程
构成的集合:“①方程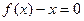 有实数根;②函数
有实数根;②函数 的导数
的导数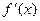 满足
满足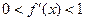 ”.
”.
(1)判断函数 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(2)若集合M中的元素具有下面的性质:“若 的定义域为D,则对于任意
的定义域为D,则对于任意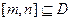 ,都存在
,都存在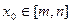 ,使得等式
,使得等式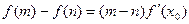 成立”,
成立”, 试用这一性质证明:方程
试用这一性质证明:方程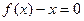 只有一个实数根;
只有一个实数根;
(3)设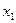 是方程
是方程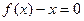 的实
的实 数根,求证:对于
数根,求证:对于 定义域中的任意的
定义域中的任意的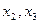 ,当
,当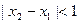 且
且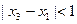 时,
时,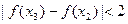 .
.
(2012年高考湖北卷理科21)(本小题满分13分)
设A是单位圆x2+y2=1上的任意一点,i是过点A与x轴垂直的直线,D是直线i与x轴的交点,点M在直线l上,且满足丨DM丨=m丨DA丨(m>0,且m≠1)。当点A在圆上运动时,记点M的轨迹为曲线C。
(I)求曲线C的方程,判断曲线C为何种圆锥曲线,并求焦点坐标;
(Ⅱ)过原点且斜率为k的直线交曲线C于P、Q两点,其中P在第一象限,它在y轴上的射影为点N,直线QN交曲线C于另一点H,是否存在m,使得对任意的k>0,都有PQ⊥PH?若存在,求m的值;若不存在,请说明理由。
(本题满分14分)集合A是由适合以下性质的函数f(x)构成的:对于定义域内任意两个不相等的实数 ,都有
,都有 .
.
(1)试判断f(x)= x2及g(x)=log2x是否在集合A中,并说明理由;
(2)设f(x)ÎA且定义域为(0,+¥),值域为(0,1), ,试求出一个满足以上条件的函数f (x)的解析式.
,试求出一个满足以上条件的函数f (x)的解析式.
一、选择题(每小题5分,共40分)
题 号
1
2
3
4
5
6
7
8
答 案
B
A
D
C
C
A
B
C
二、填空题(每小题5分,其中第一空3分,第二空2分,共30分)
9.2π; .files/image088.gif) π 10.12π;x=13π 11.
π 10.12π;x=13π 11..files/image090.gif)
12.(±2,0);-.files/image092.gif) 13.9; 41 14.12; (-6,4)
13.9; 41 14.12; (-6,4)
三、15.(本小题满分12分)
解:(1).files/image094.gif) ……………………3分
……………………3分
.files/image096.gif) ………………5分
………………5分
(2)点P的坐标为.files/image098.gif) ………………6分
………………6分
由点P在直线.files/image100.gif) 上,即
上,即.files/image102.gif) .………………9分
.………………9分
.files/image104.gif)
.files/image106.gif) ……………………12分
……………………12分
|