练习册

  • 练习册
  • 试题
    (Ⅲ)求证:. 【查看更多】

     

    题目列表(包括答案和解析)

    （Ⅰ）求证：
    sinx
    1-cosx
    =
    1+cosx
    sinx
    ；
    （Ⅱ）化简：
    tan(3π-α)
    sin(π-α)sin(
    3
    2
    π-α)
    +
    sin(2π-α)cos(α-
    7π
    2
    )
    sin(
    3π
    2
    +α)cos(2π+α)
    ．

    查看答案和解析>>

    （Ⅰ）求证：
    C
    m
    n
    =
    n
    m
    C
    m-1
    n-1
    ；
    （Ⅱ）利用第（Ⅰ）问的结果证明Cn1+2Cn2+3Cn3+…+nCnn=n•2n-1；  
    （Ⅲ）其实我们常借用构造等式，对同一个量算两次的方法来证明组合等式，譬如：（1+x）1+（1+x）2+（1+x）3+…+（1+x）n=
    (1+x)[1-(1+x)n]
    1-(1+x)
    =
    (1+x)n+1-(1+x)
    x
    ；，由左边可求得x2的系数为C22+C32+C42+…+Cn2，利用右式可得x2的系数为Cn+13，所以C22+C32+C42+…+Cn2=Cn+13．请利用此方法证明：（C2n0）2-（C2n1）2+（C2n2）2-（C2n3）2+…+（C2n2n）2=（-1）nC2nn．

    查看答案和解析>>

    （Ⅰ）求证：
    sinx
    1-cosx
    =
    1+cosx
    sinx
    ；
    （Ⅱ）化简：
    tan(3π-α)
    sin(π-α)sin(
    3
    2
    π-α)
    +
    sin(2π-α)cos(α-
    7π
    2
    )
    sin(
    3π
    2
    +α)cos(2π+α)
    ．

    查看答案和解析>>

    （Ⅰ）求证：；
    （Ⅱ）化简：．

    查看答案和解析>>

    （Ⅰ）求证：；
    （Ⅱ）利用第（Ⅰ）问的结果证明Cn1+2Cn2+3Cn3+…+nCnn=n•2n-1；  
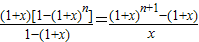    （Ⅲ）其实我们常借用构造等式，对同一个量算两次的方法来证明组合等式，譬如：（1+x）1+（1+x）2+（1+x）3+…+（1+x）n=；，由左边可求得x2的系数为C22+C32+C42+…+Cn2，利用右式可得x2的系数为Cn+13，所以C22+C32+C42+…+Cn2=Cn+13．请利用此方法证明：（C2n）2-（C2n1）2+（C2n2）2-（C2n3）2+…+（C2n2n）2=（-1）nC2nn．

    查看答案和解析>>

    一、ADBAB  CDCBC

    二、11  9   12     13  384    14     15     

    三、解答题

    16．解：（I）

           又，∴，   ……5分

         （II）

       

    17．解：(Ⅰ) 抛掷一次出现的点数共有6×6 = 36种不同结果，其中“点数之和为7”包含了 (1 , 6) , (2 , 5) , (3 , 4) , (4 , 3) , (5 , 2) , (6 , 1)共6个结果，

    ∴抛掷一次出现的点数之和为7的概率为 ………………………… 2分

    ξ可取1 , 2 , 3 , 4

    P (ξ=1) =，P (ξ=2) =，P (ξ= 3) =

    P (ξ= 4) =

    ∴ξ的概率分布列为

    ξ

    1

    2

    3

    4

    P

    …… 6分

    Eξ= 1×+ 2×+ 3×+ 4×=  …………………………… 8分

    (Ⅱ) 不限制两人抛掷的次数，甲获胜的概率为：

     P =+ ()2×+ ()4×+ … = .      ………… 12分

     

    18．解：解：（1）它是有一条侧棱垂直于底面的四棱锥      … 3分

    （注：评分注意实线、虚线；垂直关系；长度比例等）

    （2）由（1）得，6ec8aac122bd4f6e，6ec8aac122bd4f6e，得6ec8aac122bd4f6e

    6ec8aac122bd4f6e∴6ec8aac122bd4f6e，而6ec8aac122bd4f6e，6ec8aac122bd4f6e

    ∴6ec8aac122bd4f6e…………6分

    ∴6ec8aac122bd4f6e

    ∴6ec8aac122bd4f6e………8分

    又在6ec8aac122bd4f6e中，6ec8aac122bd4f6e，故6ec8aac122bd4f6e

    ∴二面角6ec8aac122bd4f6e的平面角为6ec8aac122bd4f6e… ………8分

    （3）解略。 

    19．（I）证明：   ∵  ∴   ∵，

    ∴＝

    是首项为2，公差为1的等差数列.       …………3分

    (II)解:=,     …6分

      =.   …7分

    (III)证明: ，

    .       …… 9分

        .…………12分

    20．解（Ⅰ）∵6ec8aac122bd4f6e过（0，0）    则6ec8aac122bd4f6e

    ∴∠OCA=90°，  即6ec8aac122bd4f6e  又∵6ec8aac122bd4f6e

    将C点坐标代入得  6ec8aac122bd4f6e   解得  c2=8，b2=4

    ∴椭圆m：6ec8aac122bd4f6e  …………5分

    （Ⅱ）由条件D（0，－2）  ∵M（0，t）

    1°当k=0时，显然－2<t<2  …………6分

    2°当k≠0时，设6ec8aac122bd4f6e

    6ec8aac122bd4f6e   消y得  6ec8aac122bd4f6e  

    由△>0  可得  6ec8aac122bd4f6e   ①

    设6ec8aac122bd4f6e

    则6ec8aac122bd4f6e     6ec8aac122bd4f6e   

    ∴6ec8aac122bd4f6e           …………10分

    由6ec8aac122bd4f6e 

    ∴6ec8aac122bd4f6e   ②

    ∴t>1  将①代入②得   1<t<4

    ∴t的范围是（1，4）。综上t∈（－2，4）  ………………13分

     

    21．解： (1) 依题知，得：，的方程为，

     即直线的方程是 ………………… 6分

    (2)  证明：由(1)得

    ①由于  ，所以，

    又,所以

    ②因为  ，

    且，所以，即。

    又 ，所以

    故当时，有………………… 14分

     


    同步练习册答案