
题目列表(包括答案和解析)
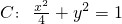 的右焦点为F,右准线为l,过F作直线交椭圆C于点P、Q两点.
的右焦点为F,右准线为l,过F作直线交椭圆C于点P、Q两点.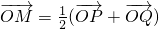 (O为坐标原点),求M的轨迹方程;
(O为坐标原点),求M的轨迹方程; 的右焦点为F,右准线为l,过F作直线交椭圆C于点P、Q两点.
的右焦点为F,右准线为l,过F作直线交椭圆C于点P、Q两点.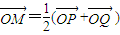 (O为坐标原点),求M的轨迹方程;
(O为坐标原点),求M的轨迹方程;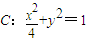 的右焦点为F,右准线为l,过F作直线交椭圆C于点P、Q两点.
的右焦点为F,右准线为l,过F作直线交椭圆C于点P、Q两点. (O为坐标原点),求M的轨迹方程;
(O为坐标原点),求M的轨迹方程;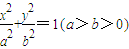 的右焦点为F(1,0),短轴的端点分别为B1,B2,且
的右焦点为F(1,0),短轴的端点分别为B1,B2,且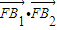 =-a.
=-a.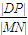 的取值范围.
的取值范围.椭圆C:![]() 的左、右焦点分别是F1.F2,离心率为
的左、右焦点分别是F1.F2,离心率为![]() 过F,且垂直于x轴的直线被椭圆C截得的线段长为l.
过F,且垂直于x轴的直线被椭圆C截得的线段长为l.
(Ⅰ)求椭圆C的方程;
(Ⅱ)点P是椭圆C上除长轴端点外的任一点,连接PF1,PF2,设∠F1PF2的角平分线PM交C的长轴于点M(m,0),求m的取值范围;
(Ⅲ)在(Ⅱ)的条件下,过点p作斜率为k的直线l,使得l与椭圆C有且只有一个公共点.
设直线PF1,PF2的斜率分别为k1,k2,若k≠0,试证明![]() 为定值,并求出这个定值.
为定值,并求出这个定值.
一、选择题:本大题共12小题,每小题5分,共60分。
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
B
A
C
B
C
B
C
C
A
A
D
二、填空题:本大题共4小题,每小题4分,共16分
13、 -1 14、 24/5 15、 16/3 16、 ① ②
解:由 得 P ( 1,-1)
得 P ( 1,-1)
据题意,直线l与直线 垂直,故l斜率
垂直,故l斜率
∴ 直线l方程为  即
即  .
.
解:连结PO,得
 当PO通过圆心时有最大值和最小值
当PO通过圆心时有最大值和最小值



解:设生产甲、乙两种肥料各 车皮,利润总额为
车皮,利润总额为 元,那么
元,那么


画图得当 时总额
时总额 的最大值为30000
的最大值为30000
解:(1)
(2) 或0
或0
解:(1)设A(x1,y1),B(x2,y2),AB的方程为y-1=k(x-2) 即y=kx+1-2k①
∵离心率e= ∴椭圆方程可化为
∴椭圆方程可化为 ②
②
将①代入②得(1+2k2)x2+4(1-2k)?kx+2(1-2k)2-2b2=0
∵x1+x2= ∴k=-1
∴k=-1
∴x1x2= 又
又 ∴
∴
即 ∴b2=8 ∴
∴b2=8 ∴
(2)设 (不妨设m<n)则由第二定义知
(不妨设m<n)则由第二定义知
即 或
或
∴ 或
或
解:由已知得 A (-1, 0 )、B ( 1, 0 ),
设 P ( x, y ), C ( x0, y0 ) , 则 D (x0, -y0 ),
由A、C、P三点共线得  ①
①
由D、B、P三点共线得  ②
②
①×② 得  ③
③
又 x02 + y02 = 1, ∴ y02 = 1-x02 代入③得 x2-y2 = 1,
即点P在双曲线x2-y2 = 1上, 故由双曲线定义知,存在两个定点E (- , 0 )、
, 0 )、
F ( , 0 )(即此双曲线的焦点),使 | | PE |-| PF | | = 2 (即此双曲线的实轴长) 为定值.
, 0 )(即此双曲线的焦点),使 | | PE |-| PF | | = 2 (即此双曲线的实轴长) 为定值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com