
��ԲC��![]() �����ҽ���ֱ���F1��F2��������Ϊ
�����ҽ���ֱ���F1��F2��������Ϊ![]() ��F���Ҵ�ֱ��x���ֱ�߱���ԲC�صõ��߶γ�Ϊl��
��F���Ҵ�ֱ��x���ֱ�߱���ԲC�صõ��߶γ�Ϊl��
(��)����ԲC�ķ��̣�
(��)��P����ԲC�ϳ�����˵������һ�㣬����PF1��PF2�����F1PF2�Ľ�ƽ����PM��C�ij����ڵ�M(m��0)����m��ȡֵ��Χ��
(��)��(��)�������£�����p��б��Ϊk��ֱ��l��ʹ��l����ԲC����ֻ��һ�������㣮
��ֱ��PF1��PF2��б�ʷֱ�Ϊk1��k2����k��0����֤��![]() Ϊ��ֵ������������ֵ��
Ϊ��ֵ������������ֵ��
 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2013•���ʶ�ģ��
��2013•���ʶ�ģ��| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
| MQ |
| QN |
| MR |
| RN |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪��ԲC��![]() �����ҽ���ΪF1��F2��������Ϊe. ֱ��
�����ҽ���ΪF1��F2��������Ϊe. ֱ��![]() ��x�ᡢy��ֱ��ڵ�A��B��M��ֱ��l����ԲC��һ�������㣬P�ǵ�F1����ֱ��l�ĶԳƵ㣬��
��x�ᡢy��ֱ��ڵ�A��B��M��ֱ��l����ԲC��һ�������㣬P�ǵ�F1����ֱ��l�ĶԳƵ㣬��![]()
����֤����![]() ��
��
������![]() ���ܳ�Ϊ6��д����ԲC�ķ���.
���ܳ�Ϊ6��д����ԲC�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013���㽭ʡ�����и߿���ѧһģ�Ծ������ƣ��������棩 ���ͣ������
 �����ҽ���ֱ�ΪF1��F2��OΪԭ�㣮
�����ҽ���ֱ�ΪF1��F2��OΪԭ�㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013��ȫ����ͨ�ߵ�ѧУ����ͳһ�����Ŀ���ѧ���¿α�2�������棩 ���ͣ�ѡ����
����ԲC�� �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ ��
�� ��P��C�ϵĵ㣬
��P��C�ϵĵ㣬 ��
��
 ��
��
�� =
= ����C���������� ��
����C���������� ��
A��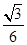 B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013������ʡ�߶���ѧ�����п���������ѧ�Ծ� ���ͣ������
����С������12�֣�����ԲC�� �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ ��
�� ����
���� ����
����
��������ԲC�������� ��
��
��������֪�� ����ֱ��
����ֱ�� ����ԲC�ཻ��A��B���㣬��
����ԲC�ཻ��A��B���㣬��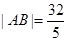 ��
��
����ԲC�ķ��̡�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com