练习册

  • 练习册
  • 试题
    例3. 如图所示.一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上.物体与斜面接触时速度与水平方向的夹角φ满足( )A.tanφ=sinθ B. tanφ=cosθC. tanφ=tanθD. tanφ=2tanθ 【查看更多】

     

    题目列表(包括答案和解析)

    （08年全国卷Ⅰ）25.（22分）如图所示，在坐标系xoy中，过原点的直线OC与x轴正向的夹角φ=120°，在OC右侧有一匀强电场：在第二、三象限内有一心强磁场，其上边界与电场边界重叠、右边界为y轴、左边界为图中平行于y轴的虚线，磁场的磁感应强度大小为B，方向垂直抵面向里。一带正电荷q、质量为m的粒子以某一速度自磁场左边界上的A点射入磁场区域，并从O点射出，粒子射出磁场的速度方向与x轴的夹角θ＝30°，大小为v，粒子在磁场中的运动轨迹为纸面内的一段圆弧，且弧的半径为磁场左右边界间距的两倍。粒子进入电场后，在电场力的作用下又由O点返回磁场区域，经过一段时间后再次离开磁场。已知粒子从A点射入到第二次离开磁场所用的时间恰好等于粒子在磁场中做圆周运动的周期。忽略重力的影响。求

    （1）粒子经过A点时速度的方向和A点到x轴的距离；

    （2）匀强电场的大小和方向；

    （3）粒子从第二次离开磁场到再次进入电场时所用的时间。

    查看答案和解析>>

    （02年全国卷）在如图所示的电路中，R1、R2、R3和R4皆为定值电阻，R5为可变电阻，电源的电动势为ε，内阻为r。设电流表A的读数为I，电压表V的读数为U。当R5的滑动触点向图中a端移动时，

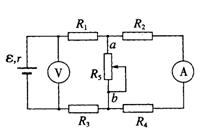
    A.I变大，U变小                    B.I变大，U变大

    C.I变小，U变大                    D.I变小，U变小

    查看答案和解析>>

    （07年全国卷Ⅱ）25.（20分）如图所示，在坐标系Oxy的第一象限中在在沿y轴正方向的匀强电场，场强大小为E。在其它象限中在在匀强磁场，磁场方向垂直于纸面向里，A是y轴上的一点，它到坐标原点O的距离为h；C是x轴上的一点，到O点的距离为l，一质量为m、电荷量为q的带负电的粒子以某一初速度沿x轴方向从A点进入电场区域，继而通过C点进入磁场区域，并再次通过A点，此时速度方向与y轴正方向成锐角。不计重力作用。试求：

    　　（1）粒子经过C点时速度的大小和方向；

    　　（2）磁感应强度的大小B。

     

    查看答案和解析>>

    （08年上海卷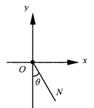）4.如图所示，在竖直平面内的直角坐标系中，一个质量为m的质点在外力F的作用下，从坐标原点O由静止沿直线ON斜向下运动，直线ON与y轴负方向成θ角（θ＜π/4）。则F大小至少为           ；若F＝mgtanθ，则质点机械能大小的变化情况是                          。

    查看答案和解析>>

    （07年全国卷Ⅱ）23.（16分）如图所示，位于竖直平面内的光滑轨道，由一段斜的直轨道的与之相切的圆形轨道连接而成，圆形轨道的半径为R。一质量为m的小物块从斜轨道上某处由静止开始下滑，然后沿圆形轨道运动。要求物块能通过圆形轨道的最高点，且在该最高点与轨道间的压力不能超过5mg（g为重力加速度）。求物块初始位置相对于圆形轨道底部的高度h的取值范围。

     

     

     

     

     

     

     

    查看答案和解析>>

     

    一、选择题

    1、根据图象分析：若沿x轴作匀速运动，通过图1分析可知，y方向先减速后加速；若沿y轴方向作匀速运动，通过图2分析可知，x方向先加速后减速。

    答案：B

    2、乙船能到达A点，则vcos600=u，

    过河时间t满足：t = H/（ vsin600）, 甲、乙两船沿垂直于河岸方向的分速度相同，故过河时间相同。在t时间内甲船沿河岸方向的位移为s= （vcos600 + u ）t=。

    答案：D

    3、根据万有引力定律：，得：T=

    答案：A

    4、质点在A、B、C、D四点离开轨道，分别做下抛、平抛、上抛、平抛运动。很明显，在A点离开轨道比在C、D两点离开轨道在空间时间短。通过计算在A点下抛落地时间为tA=（6-4）s，在B点平抛落地时间tB=4s，显然，在A点离开轨道后在空中时间最短。根据机械能守恒，在D刚抛出时机械能最大，所以落地时速度最大。

    答案：AD

    5、在轨道上向其运行方向弹射一个物体，由于质量远小于空间站的质量，空间站仍沿原方向运动。根据动量守恒，弹出后一瞬间，空间站沿原运行方向的速度变小，提供的向心力（万有引力）大于需要的向心力，轨道半径减小，高度降低，在较低的轨道上运行速率变大，周期变小。

    答案：C

    6、当悬线在竖直状态与钉相碰时根据能量守恒可知，小球速度不变；但圆周运动的半径减小，需要的向心力变大，向心加速度变大，绳子上的拉力变大。

    答案：BD

    7、根据万有引力定律：可得：M=,可求出恒星质量与太阳质量之比，根据可得：v=,可求出行星运行速度与地球公转速度之比。

    答案：AD

    8、卫星仍围绕地球运行，所以发射速度小11.2km/s；最大环绕速度为7.9km/s，所以在轨道Ⅱ上的速度小于7.9km/s；根据机械能守恒可知：卫星在P点的速度大于在Q点的速度；卫星在轨道Ⅰ的Q点是提供的向心力大于需要的向心力，在轨道Ⅱ上Q点是提供的向心力等于需要的向心力，所以在Q点从轨道Ⅰ进入轨道Ⅱ必须增大速度。

    答案：CD

    9、同步卫星随地球自转的方向是从东向西，把同步卫星从赤道上空3.6万千米、东经103°处，调整到104°处，相对于地球沿前进方向移动位置，需要增大相对速度，所以应先下降高度增大速度到某一位置再上升到原来的高度。

    答案：A

    10、开始转动时向心力由静摩擦力提供，但根据F=mrω2可知，B需要的向心力是A的两倍。所以随着转速增大，B的摩擦力首先达到最大静摩擦力。继续增大转速，绳子的张力增大，B的向心力由最大静摩擦力提供，A的向心力由静摩擦力和绳子的张力的合力提供，随着转速的增大，B需要的向心力的增量（绳子张力的增量）比A需要的向心力的增量大，因而A指向圆心的摩擦力逐渐减小直到为0然后反向增大到最大静摩擦力。所以，B受到的静摩擦力先增大，后保持不变；A受到的静摩擦力是先减小后增大；A受到的合外力就是向心力一直在增大。

    答案：BD

     

    二、填空题

    11、圆盘转动时，角速度的表达式为ω= ，  T为电磁打点计的时器打点的时间间隔，r为圆盘的半径，x2、x1是纸带上选定的两点分别对应米尺上的刻度值，n为选定的两点间的打点数（含两点）。地纸带上选取两点（间隔尽可能大些）代入上式可求得ω= 6.8rad/s。

    12、 (1)斜槽末端切线方向保持水平；从同一高度。

    （2）设时间间隔为t, x = v0t，   y2-y1=gt2 ，解得: v0=.将x=20.00cm，y1 =4.70cm， y2 =14.50cm代入求得v0=2m/s

     

    三、计算题

    13．解：⑴在行星表面，质量为m的物体的重力近似等于其受到的万有引力，则

                              

    g=                               

    得：   

    ⑵行星表面的环绕速度即为第一宇宙速度，做匀速圆周运动的向心力是万有引力提供的，则

                             

    v1=　　　　　　　　　           

    得：　

    14．解析：用r表示飞船圆轨道半径,有r =R +H=6.71×l06 m．

    由万有引力定律和牛顿定律，得 , 式中M表示地球质量，m表示飞船质量，T表示飞船绕地球运行的周期，G表示万有引力常量．

    利用及上式, 得 ，代入数值解得T=5.28×103s,

    出舱活动时间t=25min23s=1523s, 航天员绕行地球角度 =1040

     

    15．解：（1）这位同学对过程的分析错误，物块先沿着圆柱面加速下滑，然后离开圆柱面做斜下抛运动，离开圆柱面时的速率不等于。                   

    （2）a、设物块离开圆柱面时的速率为,

                         

            

    解得：                      

    （2）b、由：  得：

    落地时的速率为                       

    16.解：对子弹和木块应用动量守恒定律：

                                  

          所以                                  

    对子弹、木块由水平轨道到最高点应用机械能守恒定律，

    取水平面为零势能面：有

              

       所以                        

    由平抛运动规律有：                          

                                

    解得:                   

    所以，当R = 0.2m时水平距离最大                

    最大值Smax = 0.8m。

     

    17．解：（1）

     

    （2）设人在B1位置刚好看见卫星出现在A1位置，最后

    在B2位置看到卫星从A2位置消失，

        OA1=2OB1

    有  ∠A1OB1=∠A2OB2=π/3

    从B1到B2时间为t

    则有   

    18．解: （1）设 A、B的圆轨道半径分别为、，由题意知，A、B做匀速圆周运动的角速 度相同，设其为。由牛顿运动定律，有

    设 A、B之间的距离为，又，由上述各式得

    ，                               ①

    由万有引力定律，有

                               

    将①代入得

                               

    令

                               

    比较可得

                                                       ②

    （2）由牛顿第二定律，有

                                                       ③

    又可见星 A的轨道半径

                                                                    ④

    由②③④式解得

                                                   ⑤

    （3）将代入⑤式，得

                               

    代入数据得

                                                ⑥

    ，将其代入⑥式得

                                        ⑦

    可见，的值随 n的增大而增大，试令，得

                                               ⑧

    若使⑦式成立，则 n 必大于 2，即暗星 B 的质量必大于，由此得出结

    论：暗星有可能是黑洞。

     

     

     


    同步练习册答案