
题目列表(包括答案和解析)
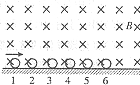 如图所示,在光滑缘水平面上由左到右沿一条直线等间距的静止排着多个形态相同的带正电的绝缘小球,依次编为为1、2、3…每个小球所带的电荷量都相等且均为q=3.75×10-3C,第一个小球的质量m=0.03kg,从第二个小球起往下的小球的质量依次为前一个小球的
如图所示,在光滑缘水平面上由左到右沿一条直线等间距的静止排着多个形态相同的带正电的绝缘小球,依次编为为1、2、3…每个小球所带的电荷量都相等且均为q=3.75×10-3C,第一个小球的质量m=0.03kg,从第二个小球起往下的小球的质量依次为前一个小球的| 1 | 3 |
| 2πm |
| B 2e |
| 1 |
| 3 |

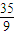 m,CD弧的半径为R=
m,CD弧的半径为R=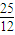 m,O为其圆心,∠COD=143°.整个装置处在水平向左的匀强电场中,电场强度大小为E=1×103N/C.一质量为m=0.4kg、电荷量为q=+3×10 -3C的物体从A点以初速度vA=15m/s沿AB轨道开始运动.若物体与轨道AB间的动摩擦因数为μ=0.2,sin37°=0.6,cos37°=0.8,g=10m/s2,物体运动过程中电荷量不变.求
m,O为其圆心,∠COD=143°.整个装置处在水平向左的匀强电场中,电场强度大小为E=1×103N/C.一质量为m=0.4kg、电荷量为q=+3×10 -3C的物体从A点以初速度vA=15m/s沿AB轨道开始运动.若物体与轨道AB间的动摩擦因数为μ=0.2,sin37°=0.6,cos37°=0.8,g=10m/s2,物体运动过程中电荷量不变.求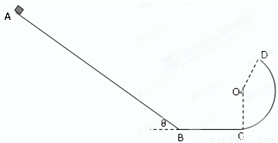
1. BCD 2. BC 3.D 4.A 5. C
6. AD 7.C 8. CD 9. AB 10.BC
11.(1)CD(2)指零 指零 指零 左偏
12. 电极A与导电纸接触不良
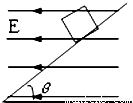
13. 解:(1)小球速度最大时,棒对它的弹力垂直于棒向下,受力分析如图,沿杆方向,电磁学中的“场”.files/image242.gif) ,垂直杆方向:
,垂直杆方向:电磁学中的“场”.files/image244.gif) ,
,电磁学中的“场”.files/image246.gif) 联立以上各式,得
联立以上各式,得电磁学中的“场”.files/image248.gif)
所以:电磁学中的“场”.files/image250.gif)
(2)小球C从斜置的绝缘棒上由静止开始运动,必须满足条件电磁学中的“场”.files/image252.gif) ,而
,而电磁学中的“场”.files/image254.gif) 即
即电磁学中的“场”.files/image256.gif) ,所以
,所以电磁学中的“场”.files/image258.gif)
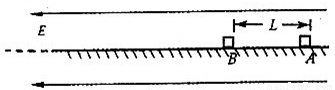
14. 解:(1)根据牛顿第二定律电磁学中的“场”.files/image260.gif) ,根据库仑定律
,根据库仑定律电磁学中的“场”.files/image262.gif) ,
,电磁学中的“场”.files/image264.gif) ,解得
,解得电磁学中的“场”.files/image266.gif)
(2)当A球受到的合力为零即加速度为零时,动能最大,设此时A球与B点间的距离为R,则电磁学中的“场”.files/image268.gif) ,解得
,解得电磁学中的“场”.files/image270.gif) 。
。
15. 解:(1)、(2)如图所示,设小球在C点的速度大小是电磁学中的“场”.files/image272.gif) ,对轨道的压力大小为
,对轨道的压力大小为电磁学中的“场”.files/image274.gif) ,则对于小球由A
,则对于小球由A电磁学中的“场”.files/image276.gif) C的过程中,应用动能定理列出:
C的过程中,应用动能定理列出:电磁学中的“场”.files/image278.gif) -0,在C点的园轨道径向应用牛顿第二定律,有
-0,在C点的园轨道径向应用牛顿第二定律,有电磁学中的“场”.files/image280.gif) ,解得
,解得电磁学中的“场”.files/image282.gif)
(3)如图所示,设小球初始位置应在离B点xm的电磁学中的“场”.files/image284.gif) 点,对小球由
点,对小球由电磁学中的“场”.files/image284.gif)
电磁学中的“场”.files/image276.gif) D的过程应用动能定理,有:
D的过程应用动能定理,有:电磁学中的“场”.files/image287.gif) ,在D点的圆轨道径向应用牛顿第二定律,有
,在D点的圆轨道径向应用牛顿第二定律,有电磁学中的“场”.files/image289.gif) ,解得
,解得电磁学中的“场”.files/image291.gif)
16. 解:(1)F1为P1参与的运动而受到指向N端的洛伦兹力,其值为:电磁学中的“场”.files/image293.gif) (其中
(其中 电磁学中的“场”.files/image295.gif) ,为
,为电磁学中的“场”.files/image297.gif) 的电量),
的电量),电磁学中的“场”.files/image297.gif) 对应有指向N端的加速度:
对应有指向N端的加速度:电磁学中的“场”.files/image300.gif) (其中m为
(其中m为电磁学中的“场”.files/image297.gif) 的质量)
的质量)
电磁学中的“场”.files/image297.gif) 在管中运动会使它受到另一个向左的洛伦兹力,此力与管壁对
在管中运动会使它受到另一个向左的洛伦兹力,此力与管壁对电磁学中的“场”.files/image297.gif) 向右的力所抵消,
向右的力所抵消,电磁学中的“场”.files/image297.gif) 到达N端时具有沿管长方向的速度:
到达N端时具有沿管长方向的速度:电磁学中的“场”.files/image302.gif)
所以,电磁学中的“场”.files/image297.gif) 对纸平面的速度大小为:
对纸平面的速度大小为: 电磁学中的“场”.files/image304.gif)
又因为电磁学中的“场”.files/image306.gif) ,故:
,故:电磁学中的“场”.files/image308.gif)
即:电磁学中的“场”.files/image310.gif)
所以电磁学中的“场”.files/image297.gif) 的比荷为:
的比荷为:电磁学中的“场”.files/image312.gif)
(2)电磁学中的“场”.files/image297.gif) 从M端到N端经历的时间为:
从M端到N端经历的时间为:电磁学中的“场”.files/image314.gif)
电磁学中的“场”.files/image297.gif) 离开管后将在纸平面上做匀速圆周运动,半径与周期分别为:
离开管后将在纸平面上做匀速圆周运动,半径与周期分别为:电磁学中的“场”.files/image316.gif)
电磁学中的“场”.files/image318.gif)
电磁学中的“场”.files/image297.gif) 经t1时间已随管朝正右方向运动:
经t1时间已随管朝正右方向运动:电磁学中的“场”.files/image320.gif)
的距离
所以电磁学中的“场”.files/image297.gif) 离开N端的位置恰好为
离开N端的位置恰好为电磁学中的“场”.files/image322.gif) 的初始位置
的初始位置
电磁学中的“场”.files/image322.gif) 经时间t1已知运动到如图所示的位置S2走过的路程为
经时间t1已知运动到如图所示的位置S2走过的路程为电磁学中的“场”.files/image325.gif)
电磁学中的“场”.files/image297.gif) 只能与
只能与电磁学中的“场”.files/image322.gif) 相碰在图中的S处,相遇时刻必为
相碰在图中的S处,相遇时刻必为
电磁学中的“场”.files/image327.gif)
且要求电磁学中的“场”.files/image322.gif) 在这段时间内恰好走过2R的路程,因此有
在这段时间内恰好走过2R的路程,因此有
电磁学中的“场”.files/image329.gif)
即得:电磁学中的“场”.files/image331.gif)
所以:电磁学中的“场”.files/image333.gif)
17. 解:电磁学中的“场”.files/image335.gif) ……①
……① 电磁学中的“场”.files/image337.gif)
由于重力和电场力平衡,电粒子在洛伦兹力作用下做圆周运动,小球平抛且碰时动量守恒,根据条件,碰后电磁学中的“场”.files/image339.gif) 反向
反向
电磁学中的“场”.files/image341.gif) ……①
……①
另有电磁学中的“场”.files/image343.gif) ……②
……②
解得电磁学中的“场”.files/image345.gif) ……③
……③
对平抛:电磁学中的“场”.files/image347.gif)
解得电磁学中的“场”.files/image349.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com