练习册

  • 练习册
  • 试题
    如图l.等腰梯形ABCD中.AD∥BC.AB=AD.∠ABC=600.E是BC的中点．如图2.将△ABE沿AE折起.使二面角B―AE―C成直二面角.连结BC.BD.F是CD的中点.P是棱BC的中点． ’ (2)求证:平面PEF⊥平面AECD, (3)判断DE能否垂直于平面ABC?并说明理由． 【查看更多】

     

    题目列表(包括答案和解析)

    (本题满分14分)

    如图1，在平面内，ABCD是的菱形，ADD``A1和CD D`C1都是正方形．将两个正方形分别沿AD，CD折起，使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面，点E是直线l上的一个动点，且与点D1位于平面ABCD同侧（图2）．

      

    (Ⅰ) 设二面角E – AC – D1的大小为q，若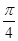£ q £ ，求线段BE长的取值范围；

    (Ⅱ)在线段上存在点，使平面平面，求与BE之间满足的关系式，并证明：当0 < BE < a时，恒有< 1．

     

    查看答案和解析>>

    (本题满分14分)如图，已知二次函数，直线l：x = 2，直线l：y = 3tx(其中1< t < 1，t为常数)；若直线l、l与函数的图象所围成的封闭图形如图(5)阴影所示．(1)求y = ；(2)求阴影面积s关于t的函数s = u(t)的解析式；(3)若过点A(1，m)(m≠4)可作曲线s=u(t)(t∈R)的三条切线，求实数m的取值范围．

    查看答案和解析>>

    (本题满分14分)

    如图1，在平面内，ABCD是的菱形，ADD``A1和CD D`C1都是正方形．将两个正方形分别沿AD，CD折起，使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面，点E是直线l上的一个动点，且与点D1位于平面ABCD同侧（图2）．

     (Ⅰ) 设二面角E – AC – D1的大小为q，若£ q £ ，求线段BE长的取值范围；

    （第20题–1）

    （第20题–2）

    (Ⅱ)在线段上存在点，使平面平面，求与BE之间满足的关系式，并证明：当0 < BE < a时，恒有< 1．

    查看答案和解析>>

    (本题满分14分)

    如图1，在平面内，ABCD是的菱形，ADD``A1和CD D`C1都是正方形．将两个正方形分别沿AD，CD折起，使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面，点E是直线l上的一个动点，且与点D1位于平面ABCD同侧（图2）．

     (Ⅰ) 设二面角E – AC – D1的大小为q，若£ q £ ，求线段BE长的取值范围；

    （第20题–1）

    （第20题–2）

    (Ⅱ)在线段上存在点，使平面平面，求与BE之间满足的关系式，并证明：当0 < BE < a时，恒有< 1．

    查看答案和解析>>

    (本题满分14分)如图所示，圆柱的高为2，底面半径为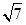,AE、DF是圆柱的两条母线，过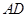作圆柱的截面交下底面于.

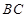    （1）求证：；

    （2）若四边形ABCD是正方形，求证；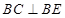

    （3）在（2）的条件下，求四棱锥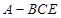的体积.

     

     

     

     

    查看答案和解析>>

    一、填空题：本大题共14小题，每小题5分，共70分．

    1．   2．   3．   4．   5．1   6．  7．  8． 9．16   10．8　  11．  12．   13．  14． ①③

    二、解答题：本大题共6小题，共90分．

    15．(1)设集合中的点为事件，  区域的面积为36，  区域的面积为18

    ．

    （2）设点在集合为事件，  甲、乙两人各掷一次骰子所得的点数为36个，其中在集合中的点有21个，故．

    16．（1）由4sinB ? sin2+ cos2B = 1 +得：

    ，          或．

    （2）法1：为锐角          

    由已知得：， 角为锐角      可得：

    由正弦定理得：．

    法2：由得：，  由余弦定理知：

    即：          ．

    17．（1）证明：连接，取中点，连接．

    在等腰梯形中，∥，AB=AD，，E是BC的中点

    与都是等边三角形   

    平面    平面

    平面    ．

    （2）证明：连接交于点，连接

    ∥，且＝    四边形是平行四边形   是线段的中点

    是线段的中点      ∥

    平面   平面．

    （3）与平面不垂直．

    证明：假设平面，  则

    平面  

    ，平面    平面   

    ，这与矛盾

    与平面不垂直．

    18．（1）设椭圆的标准方程为

    依题意得：，得   ∴  所以，椭圆的标准方程为．

    （2）设过点的直线方程为：，代入椭圆方程得;

      (*)

    依题意得：，即 

    得：，且方程的根为  

    当点位于轴上方时，过点与垂直的直线与轴交于点，

    直线的方程是：，  

    所求圆即为以线段DE为直径的圆，故方程为：

    同理可得：当点位于轴下方时，圆的方程为：．

    （3）设，由=得：，代入

    （**）    要证=，即证

    由方程组（**）可知方程组（1）成立,(2)显然成立．∴=

    19.．解（1）的解集有且只有一个元素，

    当a=4时，函数上递减

    故存在，使得不等式成立

    当a=0时，函数上递增

    故不存在，使得不等式成立

    综上，得a=4，…………………………5分

    （2）由（1）可知

    当n=1时，

    当时，

    （3），

    …

    +

                   =+>

                   >    

    20解：（1）由的定义可知，（对所有实数）等价于

    （对所有实数）这又等价于，即

    对所有实数均成立.        （*）

      由于的最大值为，

      故（*）等价于，即，这就是所求的充分必要条件

    （2）分两种情形讨论

         （i）当时，由（1）知（对所有实数）

    则由及易知，

    再由的单调性可知，

    函数在区间上的单调增区间的长度

    为（参见示意图1）

    （ii）时，不妨设，则，于是

       当时，有，从而；

    当时，有

    从而  ；

    当时，，及，由方程

          解得图象交点的横坐标为

                              ⑴

     

    显然，

    这表明在与之间。由⑴易知

     

    综上可知，在区间上，   （参见示意图2）

    故由函数及的单调性可知，在区间上的单调增区间的长度之和为，由于，即，得

              ⑵

    故由⑴、⑵得 

    综合（i）（ii）可知，在区间上的单调增区间的长度和为。

     

     

     

     

                                        

     


    同步练习册答案