练习册

  • 练习册
  • 试题
    4 设m.n是两条不同的直线.α.β.γ是三个不同的平面 给出下列四个命题:①若m⊥α.n∥α.则m⊥n, ②若α⊥γ.β⊥γ.则α∥β, 【查看更多】

     

    题目列表(包括答案和解析)

    设m、n是两条不同的直线，α、β、γ是三个不同的平面．给出下列四个命题：
    ①若m?α，α∥β，则m∥β
    ②若m、n?α，m∥β，n∥β，则α∥β
    ③若m⊥α，m⊥β，n⊥α，则n⊥β
    ④若α⊥γ，β⊥γ，m⊥α，则m⊥β
    其中，正确命题的个数是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    设m、n是两条不同的直线，α、β、γ是三个不同的平面，给出下列几个命题：

    ①若m，n是异面直线，mα，m∥β，nβ，n∥α，则α∥β；

    ②若α⊥γ，β⊥γ，则α∥β；

    ③若α⊥β，α∩β=m，n⊥m，则n⊥β；

    ④符m⊥α，n∥β且α∥β，则m⊥n．

    其中正确命题的个数为(    )

    A．1个                B．2个               C．3个               D．4个

    查看答案和解析>>

    设m、n是两条不同的直线，α、β、γ是三个不同的平面．给出下列四个命题：
    ①若m?α，α∥β，则m∥β
    ②若m、n?α，m∥β，n∥β，则α∥β
    ③若m⊥α，m⊥β，n⊥α，则n⊥β
    ④若α⊥γ，β⊥γ，m⊥α，则m⊥β
    其中，正确命题的个数是（ ）
    A．1
    B．2
    C．3
    D．4

    查看答案和解析>>

    （2013•江门一模）设m、n是两条不同的直线，α、β、γ是三个不同的平面．给出下列四个命题：
    ①若m?α，α∥β，则m∥β
    ②若m、n?α，m∥β，n∥β，则α∥β
    ③若m⊥α，m⊥β，n⊥α，则n⊥β
    ④若α⊥γ，β⊥γ，m⊥α，则m⊥β
    其中，正确命题的个数是（　　）

    查看答案和解析>>

    设l,m,n为三条不同的直线，α、β为两个不同的平面，下列命题中正确的个数是(   )

    ① 若l⊥α，m∥β，α⊥β则l⊥m ② 若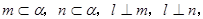则l⊥α

    ③ 若l∥m，m∥n，l⊥α，则n⊥α ④ 若l∥m，m⊥α，n⊥β，α∥β，则l∥n

    A．1                B．2                C．3                D．4

     

    查看答案和解析>>

    一、1 B     2 D    3 A   4 D     5 D     6 B   

    7 A     8  A   9 C   10 D    11 B    12 B

       二、13、3      14、-160    15、     16、  

       三、17、解: (1)     …… 3分

         的最小正周期为                        ………………… 5分

    (2) ,          …………………  7分     

                            ………………… 10分

                                    ………………… 11分

     当时,函数的最大值为1,最小值 ………… 12分

     18、（I）解：设这箱产品被用户拒绝接收事件为A,被接收为，则由对立事件概率公式

       得：

    即这箱产品被用户拒绝接收的概率为           …………   6分

    （II）                

                                       ………… 10分

    1

    2

    3

    P

                                                              …………11分

    ∴ E=                                  …………12分

    19、解法一：

    （Ⅰ）连结B1C交BC于O，则O是BC的中点，连结DO。

    ∵在△AC中，O、D均为中点，

    ∴A∥DO   …………………………2分

    ∵A平面BD，DO平面BD，

    ∴A∥平面BD。…………………4分

    （Ⅱ）设正三棱柱底面边长为2，则DC = 1。

        ∵∠DC = 60°，∴C= 。

    作DE⊥BC于E。

    ∵平面BC⊥平面ABC，

    ∴DE⊥平面BC

    作EF⊥B于F，连结DF，则 DF⊥B

    ∴∠DFE是二面角D-B-C的平面角……………………………………8分

    在Rt△DEC中，DE=

    在Rt△BFE中，EF = BE?sin

    ∴在Rt△DEF中，tan∠DFE =

    ∴二面角D－B－C的大小为arctan………………12分

    解法二：以AC的中D为原点建立坐标系，如图，

    设| AD | = 1∵∠DC =60°∴| C| = 。

         则A（1，0，0），B（0，，0），C（-1，0，0），

    （1，0）， ，

    （Ⅰ）连结C交B于O是C的中点，连结DO，则                  O.       =

    ∵A平面BD，

    ∴A∥平面BD.……………………………………………………………4分

    （Ⅱ）=（-1，0，），

           设平面BD的法向量为n = （ x , y , z ），则

           即  则有= 0令z = 1

    则n = （，0，1）…………………………………………………………8分

           设平面BC的法向量为m = ( x′ ,y′，z′)

     

    ′

    ′

    ′

    ′

          令y = -1，解得m = （，-1，0）

          二面角D ―B―C的余弦值为cos＜n , m＞＝

    ∴二面角D―B―C的大小为arc cos          …………１２分

    20、解: 对函数求导得: ……………2分

    (Ⅰ)当时,                   

    令解得 或

      解得

    所以, 单调增区间为，,

    单调减区间为(-1,1)                                    ……………5分

    (Ⅱ) 令,即,解得或     ………… 6分

    由时,列表得：

     

    x

    1

    +

    0

    －

    0

    +

    极大值

    极小值

    ……………8分

    对于时，因为,所以，

    ∴>0                                                    …………   10 分

    对于时，由表可知函数在时取得最小值

    所以，当时，                              

    由题意，不等式对恒成立，

    所以得，解得                          ……………12分

    21、解： （I）依题意知,点的轨迹是以点为焦点、直线为其相应准线,

    离心率为的椭圆

    设椭圆的长轴长为2a,短轴长为2b,焦距为2c,

    又，，∴点在x轴上,且,则3，

    解之得：,     

    ∴坐标原点为椭圆的对称中心 

    ∴动点M的轨迹方程为：                 …………    4分

    （II）设,设直线的方程为（－２〈n〈2）,代入得

                         ………… 5分

    , 

         …………  6分

    ，K（2，0）,,

    ,

     

    解得: (舍)      ∴ 直线EF在X轴上的截距为    …………8分

    （Ⅲ）设,由知, 

    直线的斜率为                …………    10分

    当时,;

    当时,,

    时取“=”）或时取“=”），

                                    

    综上所述                         …………  12分  

    22、（I）解：方程的两个根为，，

    当时，，所以；

    当时，，，所以；

    当时，，，所以时；

    当时，，，所以．    …………  4分

    （II）解：

    ．                        …………  8分

    （III）证明：，

    所以，

    ．                       …………  9分

    当时，

    ，

                                             …………  11分

    同时，

    ．                                    …………  13分

    综上，当时，．                     …………  14分

     


    同步练习册答案